Post History
It doesn't quite work that way. You are missing the fact that the current (which the magnetic field is proportional to) decays exponentially. You are also missing the resistance of the coil itsel...
#2: Post edited
- It doesn't quite work that way. You are missing the fact that the current (which the magnetic field is proportional to) decays exponentially. You are also missing the resistance of the coil itself.
- First, let's analyze what happens with just a diode. You basically have this circuit:
- 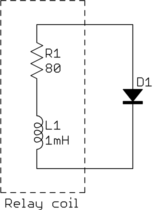
- For analysis purposes, you can think of the relay coil as a inductor and resistor in series. The resistor represents the DC resistance of the coil. The coil is a long wire all wound up. That wire has some finite resistance, whether you wrap it up into a coil or not. The inductor represents the inductance of the coil.
- Actually, first let's understand what happens if the diode weren't there and the coil was shorted. The current in the coil will decay exponentially with a time constant of
- T = L / R
- When L is in Henries, R in Ohms, then T is in seconds.
- (1 mH)/(80 Ω) = 12.5 µs
- That means that every 12.5 µs, the current decreases by a factor of e. Converting this to more intuitive units, the half-life of the current is 0.693 time constants, or 8.7 µs.
- The diode makes things more complicated. You can think of it as the diode applying a reverse voltage across the coil, in addition to the exponential caused by the resistor.
- We can get some intuition of this effect by seeing what happens if R1 weren't there. Now we have a fixed voltage applied to the coil, until the current reaches zero. That will be a linear ramp.
- (63 mA)(1 mH)/(700 mV) = 90 µs
You see by comparing this with the time constant caused by the resistor that the resistive time constant dominates for our current in this case. I'm not going to do the math to superimpose the 63 mA per 90 µs linear slope with the 8.7 µs half-life decay, but hopefully you get the general idea.- Now consider the circuit with a resistor added in series with the diode:
- 
- R1 and R2 are in series, so simply add. This is the same case as before, except that the series resistance is now 162 Ω instead of 80 Ω. Without the diode, the half-life of the current is now 4.3 µs. The linear current downramp superimposed on this due to the diode is still the same, and even less relevant due to the faster decay.
- So what does this mean to the relay? Probably not much in either case. The current has to decay to the minimum <i>holding current</i> level before the contacts even start to move apart. In most cases, the mechanical part of the relay reacts much slower than the current decays to this level. I wouldn't be surprised if it takes a few ms for the relay to open, even if the current went to 0 immediately.
- I mentioned the second circuit in another answer for completeness. Most of the time it doesn't matter, but I have seen a few cases where fast and predictable control of "high speed" relays was important. Instead of a millisecond or two being the level that matters, it was about 10 µs.
- There are very fast and nimble relays out there. When relays are built for high speed (for a relay) applications, the datasheet will go into a lot more detail on the coil properties and the response time of the mechanical parts.
- It doesn't quite work that way. You are missing the fact that the current (which the magnetic field is proportional to) decays exponentially. You are also missing the resistance of the coil itself.
- First, let's analyze what happens with just a diode. You basically have this circuit:
- 
- For analysis purposes, you can think of the relay coil as a inductor and resistor in series. The resistor represents the DC resistance of the coil. The coil is a long wire all wound up. That wire has some finite resistance, whether you wrap it up into a coil or not. The inductor represents the inductance of the coil.
- Actually, first let's understand what happens if the diode weren't there and the coil was shorted. The current in the coil will decay exponentially with a time constant of
- T = L / R
- When L is in Henries, R in Ohms, then T is in seconds.
- (1 mH)/(80 Ω) = 12.5 µs
- That means that every 12.5 µs, the current decreases by a factor of e. Converting this to more intuitive units, the half-life of the current is 0.693 time constants, or 8.7 µs.
- The diode makes things more complicated. You can think of it as the diode applying a reverse voltage across the coil, in addition to the exponential caused by the resistor.
- We can get some intuition of this effect by seeing what happens if R1 weren't there. Now we have a fixed voltage applied to the coil, until the current reaches zero. That will be a linear ramp.
- (63 mA)(1 mH)/(700 mV) = 90 µs
- You can see by comparing this with the time constant caused by the resistor, that the resistive time constant dominates for our current in this case. I'm not going to do the math to superimpose the 63 mA per 90 µs linear slope with the 8.7 µs half-life decay, but hopefully you get the general idea.
- Now consider the circuit with a resistor added in series with the diode:
- 
- R1 and R2 are in series, so simply add. This is the same case as before, except that the series resistance is now 162 Ω instead of 80 Ω. Without the diode, the half-life of the current is now 4.3 µs. The linear current downramp superimposed on this due to the diode is still the same, and even less relevant due to the faster decay.
- So what does this mean to the relay? Probably not much in either case. The current has to decay to the minimum <i>holding current</i> level before the contacts even start to move apart. In most cases, the mechanical part of the relay reacts much slower than the current decays to this level. I wouldn't be surprised if it takes a few ms for the relay to open, even if the current went to 0 immediately.
- I mentioned the second circuit in another answer for completeness. Most of the time it doesn't matter, but I have seen a few cases where fast and predictable control of "high speed" relays was important. Instead of a millisecond or two being the level that matters, it was about 10 µs.
- There are very fast and nimble relays out there. When relays are built for high speed (for a relay) applications, the datasheet will go into a lot more detail on the coil properties and the response time of the mechanical parts.
#1: Initial revision
It doesn't quite work that way. You are missing the fact that the current (which the magnetic field is proportional to) decays exponentially. You are also missing the resistance of the coil itself. First, let's analyze what happens with just a diode. You basically have this circuit:  For analysis purposes, you can think of the relay coil as a inductor and resistor in series. The resistor represents the DC resistance of the coil. The coil is a long wire all wound up. That wire has some finite resistance, whether you wrap it up into a coil or not. The inductor represents the inductance of the coil. Actually, first let's understand what happens if the diode weren't there and the coil was shorted. The current in the coil will decay exponentially with a time constant of T = L / R When L is in Henries, R in Ohms, then T is in seconds. (1 mH)/(80 Ω) = 12.5 µs That means that every 12.5 µs, the current decreases by a factor of e. Converting this to more intuitive units, the half-life of the current is 0.693 time constants, or 8.7 µs. The diode makes things more complicated. You can think of it as the diode applying a reverse voltage across the coil, in addition to the exponential caused by the resistor. We can get some intuition of this effect by seeing what happens if R1 weren't there. Now we have a fixed voltage applied to the coil, until the current reaches zero. That will be a linear ramp. (63 mA)(1 mH)/(700 mV) = 90 µs You see by comparing this with the time constant caused by the resistor that the resistive time constant dominates for our current in this case. I'm not going to do the math to superimpose the 63 mA per 90 µs linear slope with the 8.7 µs half-life decay, but hopefully you get the general idea. Now consider the circuit with a resistor added in series with the diode:  R1 and R2 are in series, so simply add. This is the same case as before, except that the series resistance is now 162 Ω instead of 80 Ω. Without the diode, the half-life of the current is now 4.3 µs. The linear current downramp superimposed on this due to the diode is still the same, and even less relevant due to the faster decay. So what does this mean to the relay? Probably not much in either case. The current has to decay to the minimum <i>holding current</i> level before the contacts even start to move apart. In most cases, the mechanical part of the relay reacts much slower than the current decays to this level. I wouldn't be surprised if it takes a few ms for the relay to open, even if the current went to 0 immediately. I mentioned the second circuit in another answer for completeness. Most of the time it doesn't matter, but I have seen a few cases where fast and predictable control of "high speed" relays was important. Instead of a millisecond or two being the level that matters, it was about 10 µs. There are very fast and nimble relays out there. When relays are built for high speed (for a relay) applications, the datasheet will go into a lot more detail on the coil properties and the response time of the mechanical parts.


















