Post History
I'm adding this as a corollary to Olin's post, in case an exact formula for attenuation is needed. That basic IIR is derived from the exponential moving average, and its impulse response is: $$h[n]...
Answer
#2: Post edited
by
Mithrandir24601
·
2020-10-25T09:34:13Z (about 4 years ago)
Added lines to mathjax
- I'm adding this as a corollary to Olin's post, in case an exact formula for attenuation is needed.
- That basic IIR is derived from the [exponential moving average](https://en.wikipedia.org/wiki/Moving_average#Exponential_moving_average), and its impulse response is:
- $$h[n]=\alpha x[n]+(1-\alpha)x[n-1]$$
- which translates into this transfer function:
- $$H(z)=\frac{\alpha}{1-(1-\alpha)z^{-1}}$$
- This can be used to determine analytically the attenuation at a particular frequency, by simply substituting \$z^{-1}=\text{e}^{-j\Omega}\$:
$$H(j\Omega)=\frac{\alpha}{1-(1-\alpha)\text{e}^{-j\Omega}} \\|H(j\Omega)|=\frac{\alpha}{\sqrt{2(\alpha-1)(\cos(\Omega)-1)+\alpha^2)}}\tag{1}$$- The -3 dB point can also be calculated from \$(1)\$:
$$|H(\Omega)|^2=\frac12=\frac{\alpha^2}{2(\alpha-1)(\cos(\Omega)-1)+\alpha^2}\quad\Rightarrow \\2(\alpha-1)(\cos(\Omega)-1)+\alpha^2=2\alpha^2\quad\Rightarrow \\\cos(\Omega)-1=\frac{\alpha^2}{2(\alpha-1)}\quad\Rightarrow \\\Omega=$$- This can be easily tested with any simulator. As an example, for \$\alpha=0.4\$, the attenuation at \$0.37\frac{f_s}{2}\$ and the -3 dB point are:
$$|H(0.37\pi)|=\frac{0.4}{\sqrt(2(0.4-1)(\cos(0.37\pi)-1)+0.4^2)}=0.4255746548210215 \\f=\frac{1}{\pi}\arccos\left(\frac{0.4^2}{2(0.4-1)}+1 ight)=0.1662579714811903$$-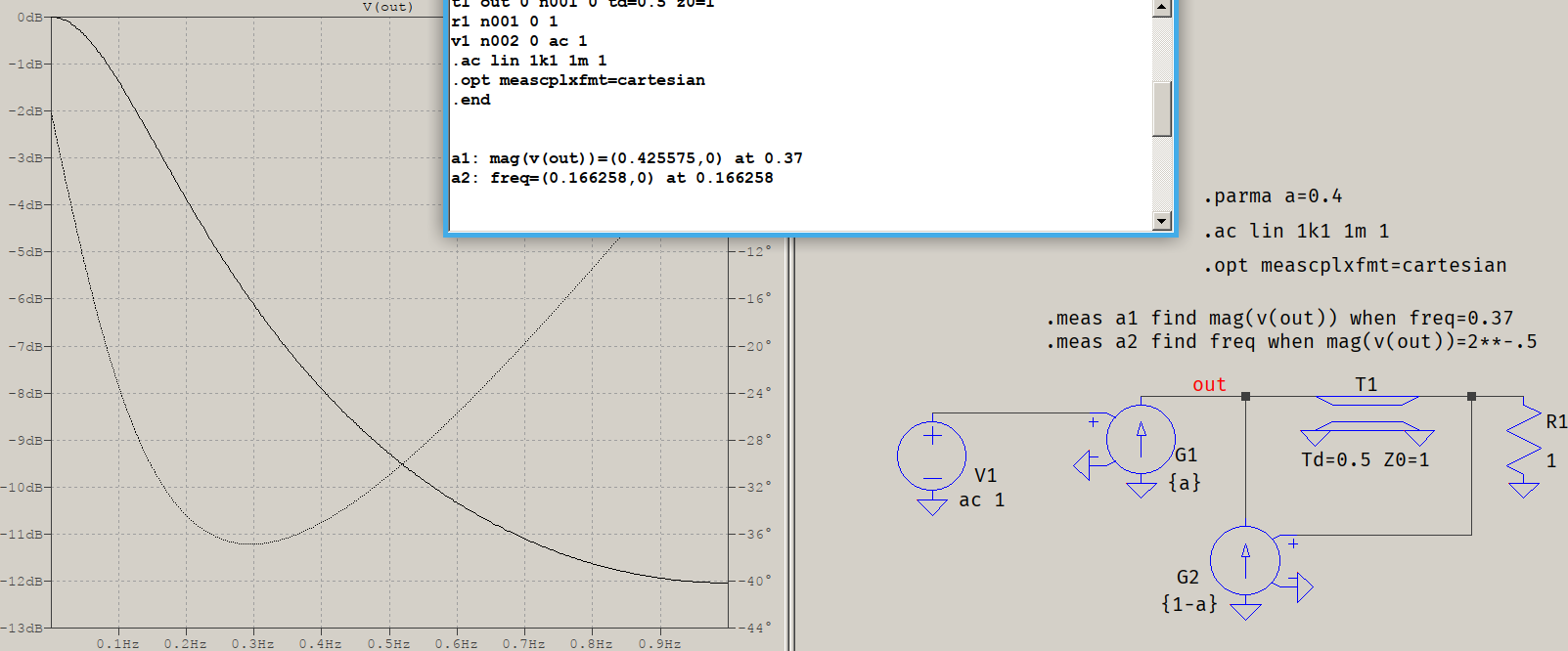 
- (where I used a normalized [0...Nyquist])
- I'm adding this as a corollary to Olin's post, in case an exact formula for attenuation is needed.
- That basic IIR is derived from the [exponential moving average](https://en.wikipedia.org/wiki/Moving_average#Exponential_moving_average), and its impulse response is:
- $$h[n]=\alpha x[n]+(1-\alpha)x[n-1]$$
- which translates into this transfer function:
- $$H(z)=\frac{\alpha}{1-(1-\alpha)z^{-1}}$$
- This can be used to determine analytically the attenuation at a particular frequency, by simply substituting \$z^{-1}=\text{e}^{-j\Omega}\$:
- \begin{align*}
- H(j\Omega)=\frac{\alpha}{1-(1-\alpha)\text{e}^{-j\Omega}} \\\ |H(j\Omega)|=\frac{\alpha}{\sqrt{2(\alpha-1)(\cos(\Omega)-1)+\alpha^2)}}\tag{1}
- \end{align*}
- The -3 dB point can also be calculated from \$(1)\$:
- \begin{align*}|H(\Omega)|^2=\frac12=\frac{\alpha^2}{2(\alpha-1)(\cos(\Omega)-1)+\alpha^2}\quad\Rightarrow \\\ 2(\alpha-1)(\cos(\Omega)-1)+\alpha^2=2\alpha^2\quad\Rightarrow \\\ \cos(\Omega)-1=\frac{\alpha^2}{2(\alpha-1)}\quad\Rightarrow \\\ \Omega=\arccos\left(1+\frac{\alpha^2}{2(\alpha-1)}\right)\end{align*}
- This can be easily tested with any simulator. As an example, for \$\alpha=0.4\$, the attenuation at \$0.37\frac{f_s}{2}\$ and the -3 dB point are:
- \begin{align*}
- |H(0.37\pi)|=\frac{0.4}{\sqrt(2(0.4-1)(\cos(0.37\pi)-1)+0.4^2)}=0.4255746548210215 \\\ f=\frac{1}{\pi}\arccos\left(\frac{0.4^2}{2(0.4-1)}+1 ight)=0.1662579714811903
- \end{align*}
- 
- (where I used a normalized [0...Nyquist])
#1: Initial revision
by
a concerned citizen
·
2020-10-23T10:20:33Z (about 4 years ago)
I'm adding this as a corollary to Olin's post, in case an exact formula for attenuation is needed.
That basic IIR is derived from the [exponential moving average](https://en.wikipedia.org/wiki/Moving_average#Exponential_moving_average), and its impulse response is:
$$h[n]=\alpha x[n]+(1-\alpha)x[n-1]$$
which translates into this transfer function:
$$H(z)=\frac{\alpha}{1-(1-\alpha)z^{-1}}$$
This can be used to determine analytically the attenuation at a particular frequency, by simply substituting \$z^{-1}=\text{e}^{-j\Omega}\$:
$$
H(j\Omega)=\frac{\alpha}{1-(1-\alpha)\text{e}^{-j\Omega}} \\
|H(j\Omega)|=\frac{\alpha}{\sqrt{2(\alpha-1)(\cos(\Omega)-1)+\alpha^2)}}\tag{1}
$$
The -3 dB point can also be calculated from \$(1)\$:
$$|H(\Omega)|^2=\frac12=\frac{\alpha^2}{2(\alpha-1)(\cos(\Omega)-1)+\alpha^2}\quad\Rightarrow \\
2(\alpha-1)(\cos(\Omega)-1)+\alpha^2=2\alpha^2\quad\Rightarrow \\
\cos(\Omega)-1=\frac{\alpha^2}{2(\alpha-1)}\quad\Rightarrow \\
\Omega=$$
This can be easily tested with any simulator. As an example, for \$\alpha=0.4\$, the attenuation at \$0.37\frac{f_s}{2}\$ and the -3 dB point are:
$$
|H(0.37\pi)|=\frac{0.4}{\sqrt(2(0.4-1)(\cos(0.37\pi)-1)+0.4^2)}=0.4255746548210215 \\
f=\frac{1}{\pi}\arccos\left(\frac{0.4^2}{2(0.4-1)}+1\right)=0.1662579714811903
$$
(where I used a normalized [0...Nyquist])