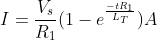Post History
When 2 inductors share the same magnetic field they become coupled and besides their self inductance they have a mutual inductance as well. For this circuit: Now current entering one coil marke...
Answer
#4: Post edited
by
Elliot Alderson
·
2021-09-04T15:40:12Z (over 3 years ago)
Fixed SI unit for henry in text, can't fix it in graphics. Fixed other small errors.
- When 2 inductors share the same magnetic field they become coupled and besides their self inductance they have a mutual inductance as well.
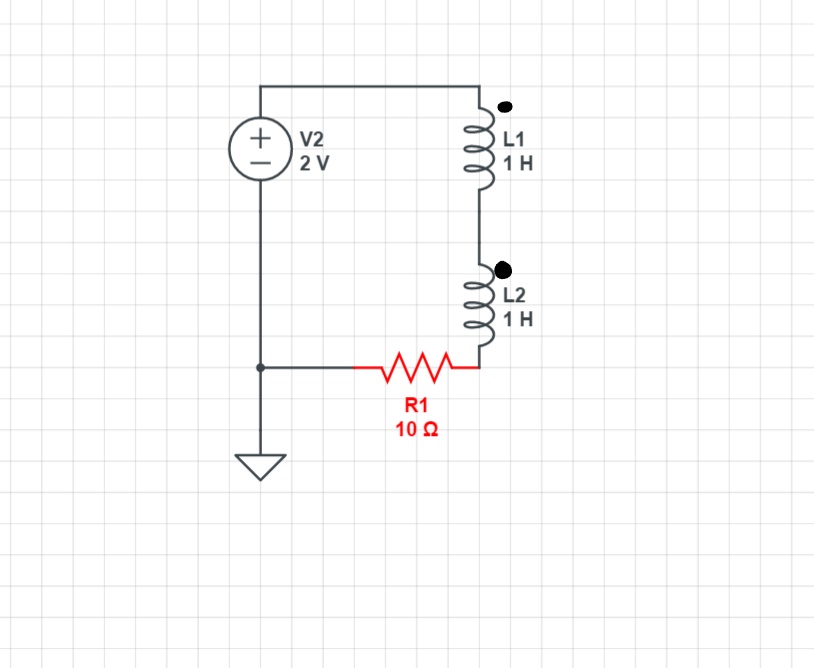
- For this circuit:
- 
Now current entering one coil marked with a dot , produces a current exitting the couple coil at its dotting end.In L1 current enters from the dotted end so this creates a current which exits from the dotted end of L2 and in L2 current enters from the dotted end so this again creates a current which exits from the dotted end of L1 so we get 2 voltage drops from self inductance of each coil and 2 voltage drops from the mutual inductance of the coupled coils.-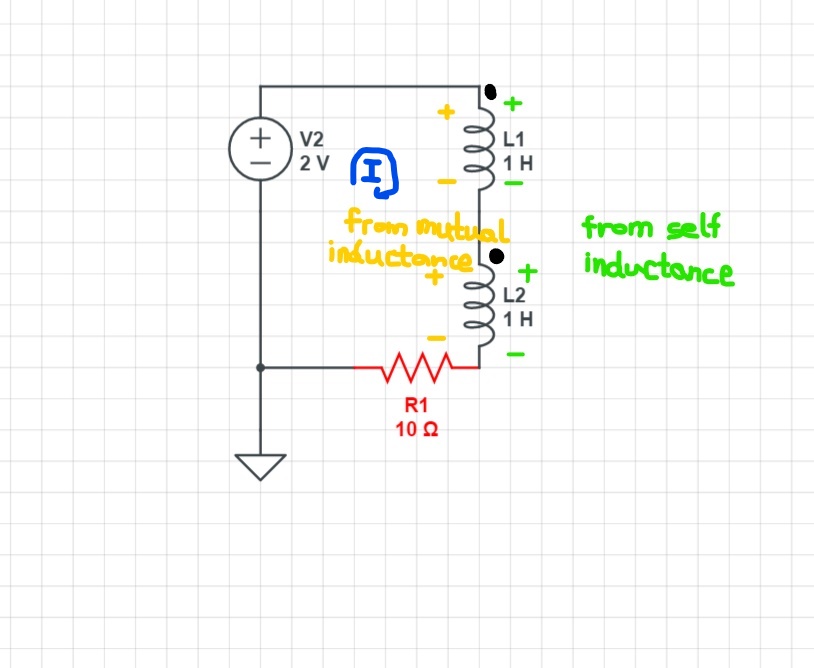 
- so that is translated to this equation:
- 
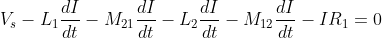
- Now obviously :
- 
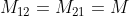
- The total inductance of the circuit becomes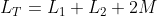 
the value of the mutual inductance is:(with k=1)-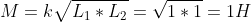 
$L_{T}=4H$- and the equation of current of this circuit becomes
- 
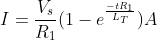
- When 2 inductors share the same magnetic field they become coupled and besides their self inductance they have a mutual inductance as well.
- For this circuit:
- 
- Now current entering one coil marked with a dot, produces a current exiting the couple coil at its dotting end. In L1 current enters from the dotted end so this creates a current which exits from the dotted end of L2 and in L2 current enters from the dotted end so this again creates a current which exits from the dotted end of L1 so we get 2 voltage drops from self inductance of each coil and 2 voltage drops from the mutual inductance of the coupled coils.
- 
- so that is translated to this equation:
- 
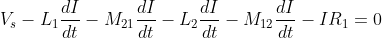
- Now obviously :
- 
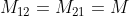
- The total inductance of the circuit becomes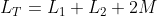 
- the value of the mutual inductance is: (with k=1)
- 
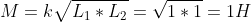
- $L_{T}=4 \text{H}$
- and the equation of current of this circuit becomes
- 
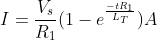
#3: Post edited
by
MissMulan
·
2021-09-03T23:13:28Z (over 3 years ago)
- When 2 inductors share the same magnetic field they become coupled and besides their self inductance they have a mutual inductance as well.
- For this circuit:
- 
- Now current entering one coil marked with a dot , produces a current exitting the couple coil at its dotting end.In L1 current enters from the dotted end so this creates a current which exits from the dotted end of L2 and in L2 current enters from the dotted end so this again creates a current which exits from the dotted end of L1 so we get 2 voltage drops from self inductance of each coil and 2 voltage drops from the mutual inductance of the coupled coils.
- 
- so that is translated to this equation:
- 
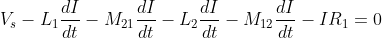
- Now obviously :
- 
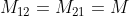
so the total inductance of the circuit becomes 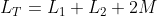- the value of the mutual inductance is:(with k=1)
- 
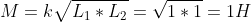
- and the equation of current of this circuit becomes
- 
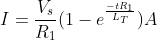
- When 2 inductors share the same magnetic field they become coupled and besides their self inductance they have a mutual inductance as well.
- For this circuit:
- 
- Now current entering one coil marked with a dot , produces a current exitting the couple coil at its dotting end.In L1 current enters from the dotted end so this creates a current which exits from the dotted end of L2 and in L2 current enters from the dotted end so this again creates a current which exits from the dotted end of L1 so we get 2 voltage drops from self inductance of each coil and 2 voltage drops from the mutual inductance of the coupled coils.
- 
- so that is translated to this equation:
- 
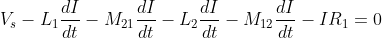
- Now obviously :
- 
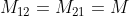
- The total inductance of the circuit becomes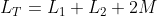 
- the value of the mutual inductance is:(with k=1)
- 
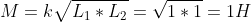
- $L_{T}=4H$
- and the equation of current of this circuit becomes
- 
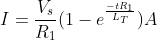
#2: Post edited
by
MissMulan
·
2021-09-03T23:11:33Z (over 3 years ago)
- When 2 inductors share the same magnetic field they become coupled and besides their self inductance they have a mutual inductance as well.
- For this circuit:
- 
- Now current entering one coil marked with a dot , produces a current exitting the couple coil at its dotting end.In L1 current enters from the dotted end so this creates a current which exits from the dotted end of L2 and in L2 current enters from the dotted end so this again creates a current which exits from the dotted end of L1 so we get 2 voltage drops from self inductance of each coil and 2 voltage drops from the mutual inductance of the coupled coils.
- 
- so that is translated to this equation:
- 
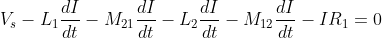
- Now obviously :
- 
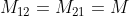
the value of the mutual inductance is:(with k=1)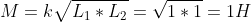- so the total inductance of the circuit becomes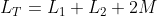 
- and the equation of current of this circuit becomes
- 
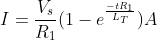
- When 2 inductors share the same magnetic field they become coupled and besides their self inductance they have a mutual inductance as well.
- For this circuit:
- 
- Now current entering one coil marked with a dot , produces a current exitting the couple coil at its dotting end.In L1 current enters from the dotted end so this creates a current which exits from the dotted end of L2 and in L2 current enters from the dotted end so this again creates a current which exits from the dotted end of L1 so we get 2 voltage drops from self inductance of each coil and 2 voltage drops from the mutual inductance of the coupled coils.
- 
- so that is translated to this equation:
- 
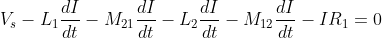
- Now obviously :
- 
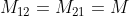
- so the total inductance of the circuit becomes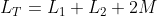 
- the value of the mutual inductance is:(with k=1)
- 
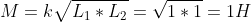
- and the equation of current of this circuit becomes
- 
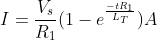
#1: Initial revision
by
MissMulan
·
2021-09-03T21:44:57Z (over 3 years ago)
When 2 inductors share the same magnetic field they become coupled and besides their self inductance they have a mutual inductance as well. For this circuit:  Now current entering one coil marked with a dot , produces a current exitting the couple coil at its dotting end.In L1 current enters from the dotted end so this creates a current which exits from the dotted end of L2 and in L2 current enters from the dotted end so this again creates a current which exits from the dotted end of L1 so we get 2 voltage drops from self inductance of each coil and 2 voltage drops from the mutual inductance of the coupled coils.  so that is translated to this equation: 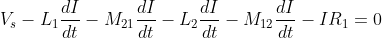 Now obviously : 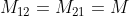 the value of the mutual inductance is:(with k=1) 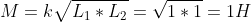 so the total inductance of the circuit becomes 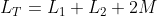 and the equation of current of this circuit becomes 