Post History
Which will be the total inductance of this circuit? Quite simply, if both the individual 1 henry inductors are perfectly magnetically coupled then, the net inductance will be 4 henries. If bot...
#6: Post edited
- > _Which will be the total inductance of this circuit?_
Quite simply, if both 1 henry inductors are perfectly magnetically coupled then the inductance will be 4 henries. If both 1 henry inductors are totally uncoupled, then the inductance will be 2 henries.This can be realized by just examining two electrically parallel windings that are 100% coupled on the same idealized magnetic core. Two parallel windings produce no-more or no-less inductance than one winding. However, each winding must take 50% of the overall current hence each winding must be regarded as having twice the inductance of the single winding scenario. Therefore, each winding must be 2 henries because, in parallel they produce a net inductance of 1 henry.- If you then disconnected the ends of the two windings and rearranged the connections so that the two windings became in series, you would find that the overall inductance has become 4 henries.
$$$$- The more important and interesting scenario is when you have two inductors of different value that are perfectly coupled. Let's say you have a 3 henry inductor in series with a 1 henry inductor: -
- 
- Starting with the inductors totally uncoupled (a net inductance of 4 henry): -
- 
- The rate of change of current is 0.25 amps per second and that is exactly what we'll get with 1 volt connected across 4 henries. However, if I added 100% coupling like this: -
- 
- The time response becomes this: -
- 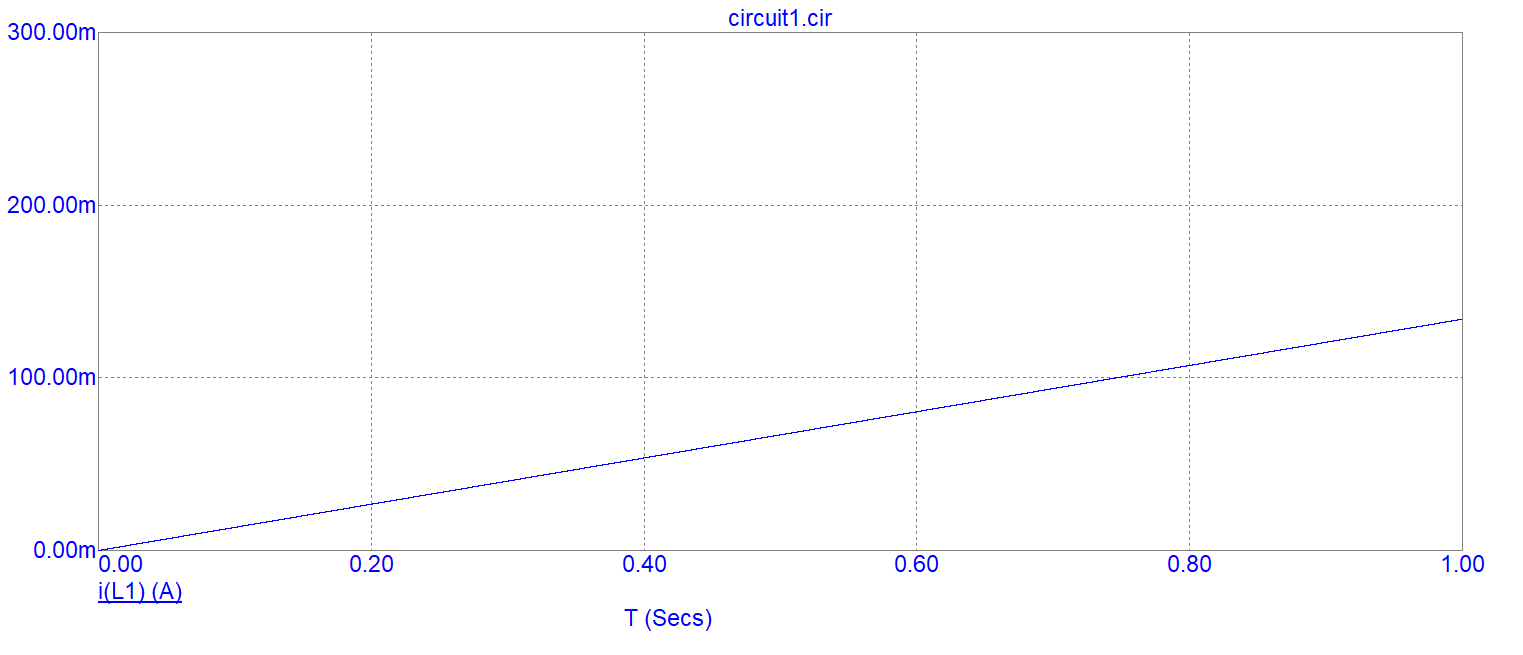
- Now, we have a rate of change of current of approximately 0.133975 amps per second (values taken from the simulator). This is an inductance value equal to the reciprocal of that value i.e. 7.4641 henries.
- Given that the mutual inductance equals \$k\cdot\sqrt{L_1 L_2} = \sqrt{3}\$ (when k=1), the net inductance is: -
- $$L_1 + L_2 + 2M = 1 + 3 + 2\sqrt3 = 7.4641 \text{ henries}$$
- -----
But, I'll tell you what, I'm not a big fan of *mutual inductance*. I mean, what does it bring to the table other than yet another formula to remember and get right. Consider this (and optionally remember it). If the two separate inductors (3 henry and 1 henry) were wound on separate but identical cores, the turns on the 3 henry inductor would be \$\sqrt3\$ times more than the turns on the 1 henry inductor.- Now, combine the turns onto one common core and you get \$1+\sqrt3\$ turns. To calculate inductance on the common core, it's just \$(1+\sqrt3)^2 =\$ 7.4641 henry. Job done without bothering to wake up mister mutual inductance.
- > _Which will be the total inductance of this circuit?_
- Quite simply, if both the individual 1 henry inductors are perfectly magnetically coupled then, the net inductance will be 4 henries. If both 1 henry inductors are totally uncoupled, then the net inductance is 2 henries.
- This can be realized by considering two electrically identical parallel windings that are 100% coupled on the same magnetic core. Two parallel windings produce no-more or no-less inductance than one winding. However, each winding must take 50% of the overall current hence each winding must be regarded as having twice the inductance of the single winding scenario.
- Therefore, each winding is 2 henries because, in parallel, they produce an inductance of 1 henry.
- If you then disconnected the ends of the two windings and rearranged the connections so that the two windings became in series, you would find that the overall inductance has become 4 henries.
- -----
- The more important and interesting scenario is when you have two inductors of different value that are perfectly coupled. Let's say you have a 3 henry inductor in series with a 1 henry inductor: -
- 
- Starting with the inductors totally uncoupled (a net inductance of 4 henry): -
- 
- The rate of change of current is 0.25 amps per second and that is exactly what we'll get with 1 volt connected across 4 henries. However, if I added 100% coupling like this: -
- 
- The time response becomes this: -
- 
- Now, we have a rate of change of current of approximately 0.133975 amps per second (values taken from the simulator). This is an inductance value equal to the reciprocal of that value i.e. 7.4641 henries.
- Given that the mutual inductance equals \$k\cdot\sqrt{L_1 L_2} = \sqrt{3}\$ (when k=1), the net inductance is: -
- $$L_1 + L_2 + 2M = 1 + 3 + 2\sqrt3 = 7.4641 \text{ henries}$$
- -----
- But, I'll tell you what, I'm not a big fan of *mutual inductance*. I mean, what does it bring to the table other than yet another formula to remember. Consider this and optionally remember it; if the two separate inductors (3 henry and 1 henry) were wound on separate but identical cores, the turns on the 3 henry inductor would be \$\sqrt3\$ times more than the turns on the 1 henry inductor.
- Now, combine the turns onto one common core and you get \$1+\sqrt3\$ turns. To calculate inductance on the common core, it's just \$(1+\sqrt3)^2 =\$ 7.4641 henry. Job done without bothering to wake up mister mutual inductance.
#5: Post edited
- > _Which will be the total inductance of this circuit?_
- Quite simply, if both 1 henry inductors are perfectly magnetically coupled then the inductance will be 4 henries. If both 1 henry inductors are totally uncoupled, then the inductance will be 2 henries.
- This can be realized by just examining two electrically parallel windings that are 100% coupled on the same idealized magnetic core. Two parallel windings produce no-more or no-less inductance than one winding. However, each winding must take 50% of the overall current hence each winding must be regarded as having twice the inductance of the single winding scenario. Therefore, each winding must be 2 henries because, in parallel they produce a net inductance of 1 henry.
- If you then disconnected the ends of the two windings and rearranged the connections so that the two windings became in series, you would find that the overall inductance has become 4 henries.
- $$$$
- The more important and interesting scenario is when you have two inductors of different value that are perfectly coupled. Let's say you have a 3 henry inductor in series with a 1 henry inductor: -
- 
- Starting with the inductors totally uncoupled (a net inductance of 4 henry): -
- 
- The rate of change of current is 0.25 amps per second and that is exactly what we'll get with 1 volt connected across 4 henries. However, if I added 100% coupling like this: -
- 
- The time response becomes this: -
- 
- Now, we have a rate of change of current of approximately 0.133975 amps per second (values taken from the simulator). This is an inductance value equal to the reciprocal of that value i.e. 7.4641 henries.
- Given that the mutual inductance equals \$k\cdot\sqrt{L_1 L_2} = \sqrt{3}\$ (when k=1), the net inductance is: -
$$L_1 + L_2 + 2M = 1 + 3 + 2\sqrt3 = 7.4641 \text{ henries}$$
- > _Which will be the total inductance of this circuit?_
- Quite simply, if both 1 henry inductors are perfectly magnetically coupled then the inductance will be 4 henries. If both 1 henry inductors are totally uncoupled, then the inductance will be 2 henries.
- This can be realized by just examining two electrically parallel windings that are 100% coupled on the same idealized magnetic core. Two parallel windings produce no-more or no-less inductance than one winding. However, each winding must take 50% of the overall current hence each winding must be regarded as having twice the inductance of the single winding scenario. Therefore, each winding must be 2 henries because, in parallel they produce a net inductance of 1 henry.
- If you then disconnected the ends of the two windings and rearranged the connections so that the two windings became in series, you would find that the overall inductance has become 4 henries.
- $$$$
- The more important and interesting scenario is when you have two inductors of different value that are perfectly coupled. Let's say you have a 3 henry inductor in series with a 1 henry inductor: -
- 
- Starting with the inductors totally uncoupled (a net inductance of 4 henry): -
- 
- The rate of change of current is 0.25 amps per second and that is exactly what we'll get with 1 volt connected across 4 henries. However, if I added 100% coupling like this: -
- 
- The time response becomes this: -
- 
- Now, we have a rate of change of current of approximately 0.133975 amps per second (values taken from the simulator). This is an inductance value equal to the reciprocal of that value i.e. 7.4641 henries.
- Given that the mutual inductance equals \$k\cdot\sqrt{L_1 L_2} = \sqrt{3}\$ (when k=1), the net inductance is: -
- $$L_1 + L_2 + 2M = 1 + 3 + 2\sqrt3 = 7.4641 \text{ henries}$$
- -----
- But, I'll tell you what, I'm not a big fan of *mutual inductance*. I mean, what does it bring to the table other than yet another formula to remember and get right. Consider this (and optionally remember it). If the two separate inductors (3 henry and 1 henry) were wound on separate but identical cores, the turns on the 3 henry inductor would be \$\sqrt3\$ times more than the turns on the 1 henry inductor.
- Now, combine the turns onto one common core and you get \$1+\sqrt3\$ turns. To calculate inductance on the common core, it's just \$(1+\sqrt3)^2 =\$ 7.4641 henry. Job done without bothering to wake up mister mutual inductance.
#4: Post edited
- > _Which will be the total inductance of this circuit?_
- Quite simply, if both 1 henry inductors are perfectly magnetically coupled then the inductance will be 4 henries. If both 1 henry inductors are totally uncoupled, then the inductance will be 2 henries.
>- This can be realized by just examining two electrically parallel windings that are 100% coupled on the same idealized magnetic core. Two parallel windings produce no-more or no-less inductance than one winding. However, each winding must take 50% of the overall current hence each winding must be regarded as having twice the inductance of the single winding scenario. Therefore, each winding must be 2 henries because, in parallel they produce a net inductance of 1 henry.
- If you then disconnected the ends of the two windings and rearranged the connections so that the two windings became in series, you would find that the overall inductance has become 4 henries.
- $$$$
- The more important and interesting scenario is when you have two inductors of different value that are perfectly coupled. Let's say you have a 3 henry inductor in series with a 1 henry inductor: -
- 
- Starting with the inductors totally uncoupled (a net inductance of 4 henry): -
- 
- The rate of change of current is 0.25 amps per second and that is exactly what we'll get with 1 volt connected across 4 henries. However, if I added 100% coupling like this: -
- 
- The time response becomes this: -
- 
- Now, we have a rate of change of current of approximately 0.133975 amps per second (values taken from the simulator). This is an inductance value equal to the reciprocal of that value i.e. 7.4641 henries.
- Given that the mutual inductance equals \$k\cdot\sqrt{L_1 L_2} = \sqrt{3}\$ (when k=1), the net inductance is: -
- $$L_1 + L_2 + 2M = 1 + 3 + 2\sqrt3 = 7.4641 \text{ henries}$$
- > _Which will be the total inductance of this circuit?_
- Quite simply, if both 1 henry inductors are perfectly magnetically coupled then the inductance will be 4 henries. If both 1 henry inductors are totally uncoupled, then the inductance will be 2 henries.
- This can be realized by just examining two electrically parallel windings that are 100% coupled on the same idealized magnetic core. Two parallel windings produce no-more or no-less inductance than one winding. However, each winding must take 50% of the overall current hence each winding must be regarded as having twice the inductance of the single winding scenario. Therefore, each winding must be 2 henries because, in parallel they produce a net inductance of 1 henry.
- If you then disconnected the ends of the two windings and rearranged the connections so that the two windings became in series, you would find that the overall inductance has become 4 henries.
- $$$$
- The more important and interesting scenario is when you have two inductors of different value that are perfectly coupled. Let's say you have a 3 henry inductor in series with a 1 henry inductor: -
- 
- Starting with the inductors totally uncoupled (a net inductance of 4 henry): -
- 
- The rate of change of current is 0.25 amps per second and that is exactly what we'll get with 1 volt connected across 4 henries. However, if I added 100% coupling like this: -
- 
- The time response becomes this: -
- 
- Now, we have a rate of change of current of approximately 0.133975 amps per second (values taken from the simulator). This is an inductance value equal to the reciprocal of that value i.e. 7.4641 henries.
- Given that the mutual inductance equals \$k\cdot\sqrt{L_1 L_2} = \sqrt{3}\$ (when k=1), the net inductance is: -
- $$L_1 + L_2 + 2M = 1 + 3 + 2\sqrt3 = 7.4641 \text{ henries}$$
#3: Post edited
- > _Which will be the total inductance of this circuit?_
- Quite simply, if both 1 henry inductors are perfectly magnetically coupled then the inductance will be 4 henries. If both 1 henry inductors are totally uncoupled, then the inductance will be 2 henries.
$$$$- This can be realized by just examining two electrically parallel windings that are 100% coupled on the same idealized magnetic core. Two parallel windings produce no-more or no-less inductance than one winding. However, each winding must take 50% of the overall current hence each winding must be regarded as having twice the inductance of the single winding scenario. Therefore, each winding must be 2 henries because, in parallel they produce a net inductance of 1 henry.
- If you then disconnected the ends of the two windings and rearranged the connections so that the two windings became in series, you would find that the overall inductance has become 4 henries.
- $$$$
- The more important and interesting scenario is when you have two inductors of different value that are perfectly coupled. Let's say you have a 3 henry inductor in series with a 1 henry inductor: -
- 
- Starting with the inductors totally uncoupled (a net inductance of 4 henry): -
- 
- The rate of change of current is 0.25 amps per second and that is exactly what we'll get with 1 volt connected across 4 henries. However, if I added 100% coupling like this: -
- 
- The time response becomes this: -
- 
- Now, we have a rate of change of current of approximately 0.133975 amps per second (values taken from the simulator). This is an inductance value equal to the reciprocal of that value i.e. 7.4641 henries.
- Given that the mutual inductance equals \$k\cdot\sqrt{L_1 L_2} = \sqrt{3}\$ (when k=1), the net inductance is: -
- $$L_1 + L_2 + 2M = 1 + 3 + 2\sqrt3 = 7.4641 \text{ henries}$$
- > _Which will be the total inductance of this circuit?_
- Quite simply, if both 1 henry inductors are perfectly magnetically coupled then the inductance will be 4 henries. If both 1 henry inductors are totally uncoupled, then the inductance will be 2 henries.
- >
- This can be realized by just examining two electrically parallel windings that are 100% coupled on the same idealized magnetic core. Two parallel windings produce no-more or no-less inductance than one winding. However, each winding must take 50% of the overall current hence each winding must be regarded as having twice the inductance of the single winding scenario. Therefore, each winding must be 2 henries because, in parallel they produce a net inductance of 1 henry.
- If you then disconnected the ends of the two windings and rearranged the connections so that the two windings became in series, you would find that the overall inductance has become 4 henries.
- $$$$
- The more important and interesting scenario is when you have two inductors of different value that are perfectly coupled. Let's say you have a 3 henry inductor in series with a 1 henry inductor: -
- 
- Starting with the inductors totally uncoupled (a net inductance of 4 henry): -
- 
- The rate of change of current is 0.25 amps per second and that is exactly what we'll get with 1 volt connected across 4 henries. However, if I added 100% coupling like this: -
- 
- The time response becomes this: -
- 
- Now, we have a rate of change of current of approximately 0.133975 amps per second (values taken from the simulator). This is an inductance value equal to the reciprocal of that value i.e. 7.4641 henries.
- Given that the mutual inductance equals \$k\cdot\sqrt{L_1 L_2} = \sqrt{3}\$ (when k=1), the net inductance is: -
- $$L_1 + L_2 + 2M = 1 + 3 + 2\sqrt3 = 7.4641 \text{ henries}$$
#2: Post edited
- > _Which will be the total inductance of this circuit?_
Quite simply, if both 1 henry inductors are perfectly magnetically coupled then the inductance will be 4 henries. If the two 1 henry inductors are totally uncoupled, then the inductance will be 2 henries.This can be realized by just examining two electrically parallel windings 100% coupled on the same idealized magnetic core. Two parallel windings produce no-more or no-less inductance than one winding. However, each winding must take 50% of the overall current hence each winding must be regarded as having twice the inductance of a single separate winding. Therefore, each winding must be 2 henries because, in parallel they produce a net inductance of 1 henry.- If you then disconnected the ends of the two windings and rearranged the connections so that the two windings became in series, you would find that the overall inductance has become 4 henries.
- The more important and interesting scenario is when you have two inductors of different value that are perfectly coupled. Let's say you have a 3 henry inductor in series with a 1 henry inductor: -
- 
So, what if we simulated this scenario, starting with the inductors totally uncoupled (a net inductance of 4 henry): -- 
- The rate of change of current is 0.25 amps per second and that is exactly what we'll get with 1 volt connected across 4 henries. However, if I added 100% coupling like this: -
- 
The time response is this: -- 
Now, we have a rate of change of current of approximately 0.133975 amps per second (values taken from the simulator). This of course is an inductance of the reciprocal of that value i.e. 7.4641 henries.Given that the mutual coupling equals \$k\cdot\sqrt{L_1 L_2} = \sqrt{3}\$ when k=1, the net inductance is: -- $$L_1 + L_2 + 2M = 1 + 3 + 2\sqrt3 = 7.4641 \text{ henries}$$
- > _Which will be the total inductance of this circuit?_
- Quite simply, if both 1 henry inductors are perfectly magnetically coupled then the inductance will be 4 henries. If both 1 henry inductors are totally uncoupled, then the inductance will be 2 henries.
- $$$$
- This can be realized by just examining two electrically parallel windings that are 100% coupled on the same idealized magnetic core. Two parallel windings produce no-more or no-less inductance than one winding. However, each winding must take 50% of the overall current hence each winding must be regarded as having twice the inductance of the single winding scenario. Therefore, each winding must be 2 henries because, in parallel they produce a net inductance of 1 henry.
- If you then disconnected the ends of the two windings and rearranged the connections so that the two windings became in series, you would find that the overall inductance has become 4 henries.
- $$$$
- The more important and interesting scenario is when you have two inductors of different value that are perfectly coupled. Let's say you have a 3 henry inductor in series with a 1 henry inductor: -
- 
- Starting with the inductors totally uncoupled (a net inductance of 4 henry): -
- 
- The rate of change of current is 0.25 amps per second and that is exactly what we'll get with 1 volt connected across 4 henries. However, if I added 100% coupling like this: -
- 
- The time response becomes this: -
- 
- Now, we have a rate of change of current of approximately 0.133975 amps per second (values taken from the simulator). This is an inductance value equal to the reciprocal of that value i.e. 7.4641 henries.
- Given that the mutual inductance equals \$k\cdot\sqrt{L_1 L_2} = \sqrt{3}\$ (when k=1), the net inductance is: -
- $$L_1 + L_2 + 2M = 1 + 3 + 2\sqrt3 = 7.4641 \text{ henries}$$
#1: Initial revision
> _Which will be the total inductance of this circuit?_
Quite simply, if both 1 henry inductors are perfectly magnetically coupled then the inductance will be 4 henries. If the two 1 henry inductors are totally uncoupled, then the inductance will be 2 henries.
This can be realized by just examining two electrically parallel windings 100% coupled on the same idealized magnetic core. Two parallel windings produce no-more or no-less inductance than one winding. However, each winding must take 50% of the overall current hence each winding must be regarded as having twice the inductance of a single separate winding. Therefore, each winding must be 2 henries because, in parallel they produce a net inductance of 1 henry.
If you then disconnected the ends of the two windings and rearranged the connections so that the two windings became in series, you would find that the overall inductance has become 4 henries.
The more important and interesting scenario is when you have two inductors of different value that are perfectly coupled. Let's say you have a 3 henry inductor in series with a 1 henry inductor: -

So, what if we simulated this scenario, starting with the inductors totally uncoupled (a net inductance of 4 henry): -

The rate of change of current is 0.25 amps per second and that is exactly what we'll get with 1 volt connected across 4 henries. However, if I added 100% coupling like this: -

The time response is this: -

Now, we have a rate of change of current of approximately 0.133975 amps per second (values taken from the simulator). This of course is an inductance of the reciprocal of that value i.e. 7.4641 henries.
Given that the mutual coupling equals \$k\cdot\sqrt{L_1 L_2} = \sqrt{3}\$ when k=1, the net inductance is: -
$$L_1 + L_2 + 2M = 1 + 3 + 2\sqrt3 = 7.4641 \text{ henries}$$


















