Post History

So here's the thing. Energy doesn't "propagate" as the video suggests. Energy is used. A voltage potential may propagate, but a voltage potential is not energy.

**Considering the video**   

With the diagram shown in the video, the electric potential is greatest between the switch and its contacts at t=0. after t=0 the switch is connected, and the high density of free electrons between the left side of the switch and the battery will exert a force on the lower density of free electrons everywhere else. As they do this, the electrons move, creating a current. this current moves the voltage potential from the switch, and spreads it out proportionally among the resistances in the circuit. As stated in the video, the wire has resistance 0, and as such this voltage potential need only spread out to the lamp itself, after which current can flow normally. The question then becomes, how fast does this happen. 

**Propagation**  
Propagation in electronics is how fast a voltage potential (aka charge density) can travel from one location to another. Propagation is limited, but often not determined by, indeed, the speed of light 'c'. Light are the same phenomena I just described; A voltage potential moving from one point to another. As a matter of fact, if we tuned the natural parameters (R,L,C, and to some extent the shape) of the wires correctly, and could make the switch flip fast enough, then this moving voltage potential could indeed send radio waves, and sometimes very effectively. Radio waves aside, you may have noticed that I said 'not often determined by' the speed of light, and that is because of a natural quality of all things called magnetic permeability. Magnetic permeability is something that everything has (including empty space!), and there is a universal minimum for this number. It is this quality specifically which limits how fast an electric potential may charge. For engineering purposes, you must know that this defines inductance, and inductance defines the rate at which current can change. For a more abstract approach, you can attempt to derive this equation from [Maxwell's Equations](https://en.wikipedia.org/wiki/Maxwell%27s_equations):

![Image alt text](https://electrical.codidact.com/uploads/uj2A8PGJBrDXQeNgtVF4fYvo)

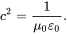
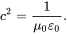
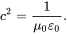Where mu 0 is the magnetic permittivity of a vacuum.

**conclusion**

This answer really only holds true if the wires were made of free space. The inductance of a wire cannot be zero, and that by default, adds time to lighting the bulb. This is admitted in the video.

The video however, assumes that the switch and the battery are one in the same, which they are not, and this also adds some propagation delay. 

Going from the initial question to the final answer, there's a lot of goal posting, and under some theoretical conditions 1/c could be the right answer. However, there is no condition in real life where these conditions could come close to the theoretical time, and further there's no way to derive an accurate guess for this question based on the info given before they ask for an answer. 

**So what conditions is the answer correct**

The closest way that we could arrive at a 1/C time, would be to ask the battery to be an RF source, and the wire itself to be a receiver. There are a lot more parameters which could be specified, but in general, this is the answer that the video really asks you to come to.