Post History
Homework problem A MOSFET has a power dissipation of $P_{d} = 10\text{W}$. The MOSFET is mounted on a heatsink. There is an isolation pad between the MOSFET case and the heatsink. We are given t...
#3: Post edited
by
Lorenzo Donati
·
2023-08-12T15:18:28Z (over 1 year ago)
Retagged.
#2: Post edited
by
Olin Lathrop
·
2022-02-25T20:11:01Z (over 2 years ago)
Always be clear about something being homework, when it is.
- > A MOSFET has a power dissipation of $P_{d} = 10\text{W}$. The MOSFET is mounted on a heatsink. There is an isolation pad between the MOSFET case and the heatsink. We are given the thermal resistances: -
- >
- > Junction to case: $R_{th,jc}= 1.7 \: \frac{°\text{C}}{\text{W}}$
- >
- > Isolation pad: $R_{th,cs}= 1.3 \: \frac{°\text{C}}{\text{W}}$
- >
- > Heatsink to ambient air: $R_{th,sa}= 2.0 \: \frac{°\text{C}}{\text{W}}$
- >
- > The ambient temperature around the MOSFET is 25°C. What is the temperature of the MOSFET case?
- **My attempt**
- The scenario must look something like this: -
- 
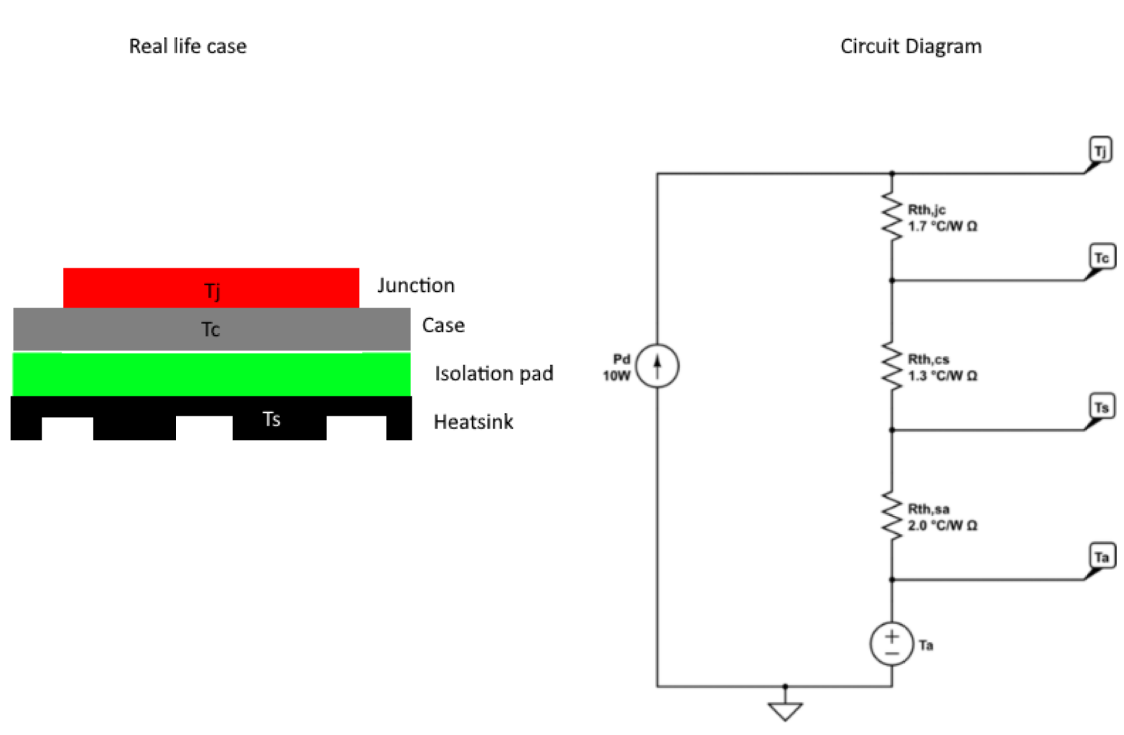
- Here I have represented the thermal resistances as resistors, the dissipated power as a current source, and the temperatures as potentials. From this I calculate the following: -
- $$P_d = \frac{T_c-T_a}{R_{th,cs}+R_{th,sa}} \Leftrightarrow$$
- $$T_c = P_d(R_{th,cs}+R_{th,sa})+T_a = (10\cdot 3.3)°C + 25°C = 58°C$$
- So the case must be 58°C.
- Is my thought process/calculations correct or have I misunderstood something? Moreover, are calculations like these useful/used when designing circuits or are they only good for "back of the envelope" calculations?
- **Homework problem**
- > A MOSFET has a power dissipation of $P_{d} = 10\text{W}$. The MOSFET is mounted on a heatsink. There is an isolation pad between the MOSFET case and the heatsink. We are given the thermal resistances: -
- >
- > Junction to case: $R_{th,jc}= 1.7 \: \frac{°\text{C}}{\text{W}}$
- >
- > Isolation pad: $R_{th,cs}= 1.3 \: \frac{°\text{C}}{\text{W}}$
- >
- > Heatsink to ambient air: $R_{th,sa}= 2.0 \: \frac{°\text{C}}{\text{W}}$
- >
- > The ambient temperature around the MOSFET is 25°C. What is the temperature of the MOSFET case?
- **My attempt**
- The scenario must look something like this: -
- 
- Here I have represented the thermal resistances as resistors, the dissipated power as a current source, and the temperatures as potentials. From this I calculate the following: -
- $$P_d = \frac{T_c-T_a}{R_{th,cs}+R_{th,sa}} \Leftrightarrow$$
- $$T_c = P_d(R_{th,cs}+R_{th,sa})+T_a = (10\cdot 3.3)°C + 25°C = 58°C$$
- So the case must be 58°C.
- Is my thought process/calculations correct or have I misunderstood something? Moreover, are calculations like these useful/used when designing circuits or are they only good for "back of the envelope" calculations?
#1: Initial revision
by
Carl
·
2022-02-25T17:54:04Z (over 2 years ago)
Case temperature of MOSFET
> A MOSFET has a power dissipation of $P_{d} = 10\text{W}$. The MOSFET is mounted on a heatsink. There is an isolation pad between the MOSFET case and the heatsink. We are given the thermal resistances: -
>
> Junction to case: $R_{th,jc}= 1.7 \: \frac{°\text{C}}{\text{W}}$
>
> Isolation pad: $R_{th,cs}= 1.3 \: \frac{°\text{C}}{\text{W}}$
>
> Heatsink to ambient air: $R_{th,sa}= 2.0 \: \frac{°\text{C}}{\text{W}}$
>
> The ambient temperature around the MOSFET is 25°C. What is the temperature of the MOSFET case?
**My attempt**
The scenario must look something like this: -
Here I have represented the thermal resistances as resistors, the dissipated power as a current source, and the temperatures as potentials. From this I calculate the following: -
$$P_d = \frac{T_c-T_a}{R_{th,cs}+R_{th,sa}} \Leftrightarrow$$
$$T_c = P_d(R_{th,cs}+R_{th,sa})+T_a = (10\cdot 3.3)°C + 25°C = 58°C$$
So the case must be 58°C.
Is my thought process/calculations correct or have I misunderstood something? Moreover, are calculations like these useful/used when designing circuits or are they only good for "back of the envelope" calculations?