Post History
It depends on whther the stages are buffered, or not. If they are buffered then it's more simple, because an RC lowpass has the transfer function: $$H_1(s)=\dfrac{\dfrac{1}{RC}}{s+\dfrac{1}{RC}}=\...
Answer
#2: Post edited
by
a concerned citizen
·
2022-10-17T18:50:06Z (about 2 years ago)
corrections
- It depends on whther the stages are buffered, or not. If they are buffered then it's more simple, because an RC lowpass has the transfer function:
- $$H_1(s)=\dfrac{\dfrac{1}{RC}}{s+\dfrac{1}{RC}}=\dfrac{1}{sRC+1} \tag{1}$$
- And adding $N$ stages will mean $H(s)$ will simply be multiplied $N$ times, thus the overall result will be:
- $$H(s)=\left\(\dfrac{1}{sRC+1}\right\)^N \tag{2}$$
- Since the result of cascading is a simple exponentiation it results that the corner frequency will remain the same, but the attenuation will be $3N\space\text{dB}$ (for integer $N$).
- If the stages are *not* buffered then you need to derive the transfer function for each final filter, since all the stages are influenced by the presence of both the previous, and the following ones. That's the sin of the passive filters. For example, for 2-, 3-, and 4-stages, once you solve for KCL/KVL/etc, you will get these transfer functions (considering $R=1,\space C=1$):
- $$\begin{align}
- H_2(s)&=\dfrac{1}{s^2+3s+1} \\\\
- H_3(s)&=\dfrac{1}{s^3+5s^2+6s+1} \\\\
- H_4(s)&=\dfrac{1}{s^4+7s^3+15s^2+10s+1}
- \end{align}$$
- Since forming the system of equations and then solving tend to take some time (even when automated), it's better to look for patterns. In this case, if you search on [OEIS](https://oeis.org/) for the sequences in the denominators, you get to [this page](https://oeis.org/search?q=1%2C3%2C1%3B1%2C5%2C6%2C1%3B1%2C7%2C15%2C10%2C1&language=english&go=Search), which gives a nice, convenient formula for generating your transfer function:
$$H_n(s)=\dfrac{1}{\binom{2n-k}{k}s},\quad k=0 ... n,\quad n\ge 0$$- BTW, for the buffered stages, the pattern will be the regular $\binom{n}{k}$, since it's a simple expansion of $(x+1)^N$.
- The Bode plots will be worse than the buffered stages, and they will be getting much worse with increasing $N$. Here is how the 1-, 2-, 3-, 4-stages look for buffered (red) vs unbuffered (blue):
- 
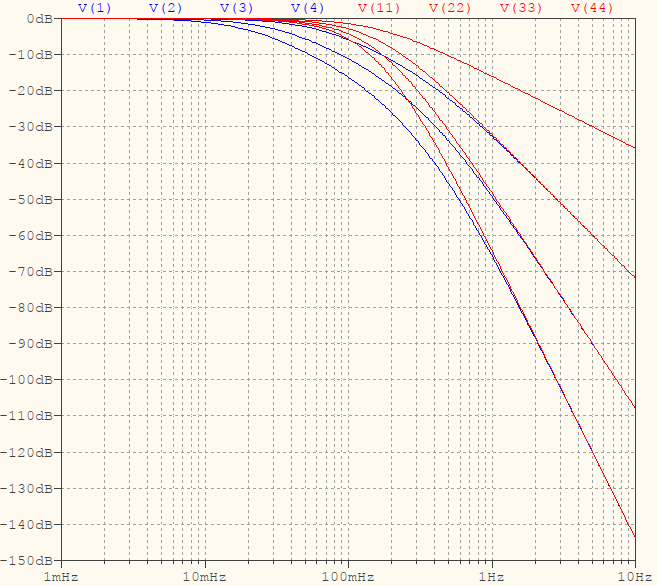
- The analytic values of the attenuations will be messier the higher the $N$, but you can still make your own test cases, mathematical or SPICE simulators, and you can see that the rate is approximately 6.3...6.5 dB/stage.
- It depends on whther the stages are buffered, or not. If they are buffered then it's more simple, because an RC lowpass has the transfer function:
- $$H_1(s)=\dfrac{\dfrac{1}{RC}}{s+\dfrac{1}{RC}}=\dfrac{1}{sRC+1} \tag{1}$$
- And adding $N$ stages will mean $H(s)$ will simply be multiplied $N$ times, thus the overall result will be:
- $$H(s)=\left\(\dfrac{1}{sRC+1}\right\)^N \tag{2}$$
- Since the result of cascading is a simple exponentiation it results that the corner frequency will remain the same, but the attenuation will be $3N\space\text{dB}$ (for integer $N$).
- If the stages are *not* buffered then you need to derive the transfer function for each final filter, since all the stages are influenced by the presence of both the previous, and the following ones. That's the sin of the passive filters. For example, for 2-, 3-, and 4-stages, once you solve for KCL/KVL/etc, you will get these transfer functions (considering $R=1,\space C=1$):
- $$\begin{align}
- H_2(s)&=\dfrac{1}{s^2+3s+1} \\\\
- H_3(s)&=\dfrac{1}{s^3+5s^2+6s+1} \\\\
- H_4(s)&=\dfrac{1}{s^4+7s^3+15s^2+10s+1}
- \end{align}$$
- Since forming the system of equations and then solving tend to take some time (even when automated), it's better to look for patterns. In this case, if you search on [OEIS](https://oeis.org/) for the sequences in the denominators, you get to [this page](https://oeis.org/search?q=1%2C3%2C1%3B1%2C5%2C6%2C1%3B1%2C7%2C15%2C10%2C1&language=english&go=Search), which gives a nice, convenient formula for generating your transfer function:
- $$H_n(s)=\dfrac{1}{\binom{2n-k}{k}s^{n-k}},\quad k=0 ... n,\quad n\ge 0$$
- BTW, for the buffered stages, the pattern will be the regular $\binom{n}{k}$, since it's a simple expansion of $(x+1)^N$.
- The Bode plots will be worse than the buffered stages, and they will be getting much worse with increasing $N$. Here is how the 1-, 2-, 3-, 4-stages look for buffered (red) vs unbuffered (blue):
- 
- The analytic values of the attenuations will be messier the higher the $N$, but you can still make your own test cases, mathematical or SPICE simulators, and you can see that the rate is approximately 6.3...6.5 dB/stage.
#1: Initial revision
by
a concerned citizen
·
2022-07-07T00:05:33Z (over 2 years ago)
It depends on whther the stages are buffered, or not. If they are buffered then it's more simple, because an RC lowpass has the transfer function:
$$H_1(s)=\dfrac{\dfrac{1}{RC}}{s+\dfrac{1}{RC}}=\dfrac{1}{sRC+1} \tag{1}$$
And adding $N$ stages will mean $H(s)$ will simply be multiplied $N$ times, thus the overall result will be:
$$H(s)=\left\(\dfrac{1}{sRC+1}\right\)^N \tag{2}$$
Since the result of cascading is a simple exponentiation it results that the corner frequency will remain the same, but the attenuation will be $3N\space\text{dB}$ (for integer $N$).
If the stages are *not* buffered then you need to derive the transfer function for each final filter, since all the stages are influenced by the presence of both the previous, and the following ones. That's the sin of the passive filters. For example, for 2-, 3-, and 4-stages, once you solve for KCL/KVL/etc, you will get these transfer functions (considering $R=1,\space C=1$):
$$\begin{align}
H_2(s)&=\dfrac{1}{s^2+3s+1} \\\\
H_3(s)&=\dfrac{1}{s^3+5s^2+6s+1} \\\\
H_4(s)&=\dfrac{1}{s^4+7s^3+15s^2+10s+1}
\end{align}$$
Since forming the system of equations and then solving tend to take some time (even when automated), it's better to look for patterns. In this case, if you search on [OEIS](https://oeis.org/) for the sequences in the denominators, you get to [this page](https://oeis.org/search?q=1%2C3%2C1%3B1%2C5%2C6%2C1%3B1%2C7%2C15%2C10%2C1&language=english&go=Search), which gives a nice, convenient formula for generating your transfer function:
$$H_n(s)=\dfrac{1}{\binom{2n-k}{k}s},\quad k=0 ... n,\quad n\ge 0$$
BTW, for the buffered stages, the pattern will be the regular $\binom{n}{k}$, since it's a simple expansion of $(x+1)^N$.
The Bode plots will be worse than the buffered stages, and they will be getting much worse with increasing $N$. Here is how the 1-, 2-, 3-, 4-stages look for buffered (red) vs unbuffered (blue):
The analytic values of the attenuations will be messier the higher the $N$, but you can still make your own test cases, mathematical or SPICE simulators, and you can see that the rate is approximately 6.3...6.5 dB/stage.