Post History
I have been trying to model this oscillator I was wondering if we can somehow predict the frequency of the oscillations.For small currents inside a diode from the Shockley diode equation $$ e^{x...
#4: Post edited
by
Lorenzo Donati
·
2023-08-09T11:33:32Z (over 1 year ago)
Retagged.
#3: Post edited
by
MissMulan
·
2022-07-20T21:14:56Z (over 2 years ago)
- I have been trying to model this oscillator
- I was wondering if we can somehow predict the frequency of the oscillations.For small currents inside a diode from the Shockley diode equation $$ e^{x}-1 = x$$ -> $$I_{D} = \frac{x}{V_{T}}I_{s} \rightarrow \frac{x}{I_{d} } = \frac{V_{T}}{I_{s}}$$ so we can say that for small currents the diode can be replaced with a resistor equal to $$R_{d} = \frac{V_{T}}{I_{s}}$$
- Now back to the relaxation oscillator circuit the 2 resistors bias the voltage of the tunnel diode well below $$V_{f}$$ of the tunnel diode so the approximation is valid.But the VI curve of the resistor which replaces the tunnel diode in order to copy the negative differential resistance region must not be a continuous function , it must be discontinuous for voltages from Vp to Vf .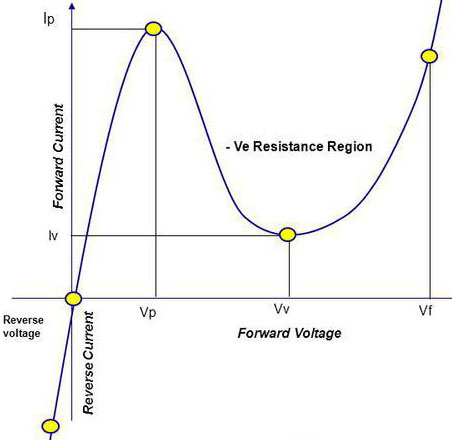
- Can we estimate that way the frequency of the relaxation oscillator?
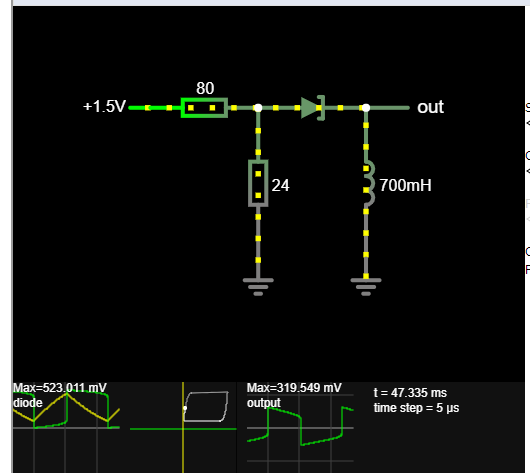
- I have been trying to model this oscillator
- 
- I was wondering if we can somehow predict the frequency of the oscillations.For small currents inside a diode from the Shockley diode equation $$ e^{x}-1 = x$$ -> $$I_{D} = \frac{x}{V_{T}}I_{s} \rightarrow \frac{x}{I_{d} } = \frac{V_{T}}{I_{s}}$$ so we can say that for small currents the diode can be replaced with a resistor equal to $$R_{d} = \frac{V_{T}}{I_{s}}$$
- Now back to the relaxation oscillator circuit the 2 resistors bias the voltage of the tunnel diode well below $$V_{f}$$ of the tunnel diode so the approximation is valid.But the VI curve of the resistor which replaces the tunnel diode in order to copy the negative differential resistance region must not be a continuous function , it must be discontinuous for voltages from Vp to Vf .
- Can we estimate that way the frequency of the relaxation oscillator?
#2: Post edited
by
MissMulan
·
2022-07-20T13:20:34Z (over 2 years ago)
Modelliing tunnel diode relaxation oscillator
- Modelling tunnel diode relaxation oscillator
#1: Initial revision
by
MissMulan
·
2022-07-20T13:18:55Z (over 2 years ago)
Modelliing tunnel diode relaxation oscillator
I have been trying to model this oscillator
I was wondering if we can somehow predict the frequency of the oscillations.For small currents inside a diode from the Shockley diode equation $$ e^{x}-1 = x$$ -> $$I_{D} = \frac{x}{V_{T}}I_{s} \rightarrow \frac{x}{I_{d} } = \frac{V_{T}}{I_{s}}$$ so we can say that for small currents the diode can be replaced with a resistor equal to $$R_{d} = \frac{V_{T}}{I_{s}}$$
Now back to the relaxation oscillator circuit the 2 resistors bias the voltage of the tunnel diode well below $$V_{f}$$ of the tunnel diode so the approximation is valid.But the VI curve of the resistor which replaces the tunnel diode in order to copy the negative differential resistance region must not be a continuous function , it must be discontinuous for voltages from Vp to Vf .
Can we estimate that way the frequency of the relaxation oscillator?