Post History
This is the circuit I have decided to use: The cut-off voltage will be just above 6 V. MOSFETs used are SiRA14BDP and the voltage supervisor is TS831. Maximum current consumption of TS831 is jus...
Answer
#2: Post edited
by
Stefan
·
2022-08-02T19:22:16Z (over 1 year ago)
- This is the circuit I have decided to use:
- The cut-off voltage will be just above 6 V. MOSFETs used are [SiRA14BDP](https://www.vishay.com/docs/76789/sira14bdp.pdf) and the voltage supervisor is [TS831](https://www.st.com/en/reset-and-supervisor-ics/ts831.html). Maximum current consumption of TS831 is just 12 uA.
- For the voltage on one cell to hit dangerous level it needs to drop from 3 V to 2.5 V. From discharge rate characteristics of any 18650 cell we can get its capacity in voltage range 3 - 2.5 V. It will be anywhere from 0.1 Ah to 0.5 Ah. If we assume the worst case, the approximation for how long it will take for the cell to hit dangerous level is:
- $$Time = \frac{Capacity}{I} = \frac{0.1 ~ Ah}{1\cdot 10^{-6} ~ A+12\cdot 10^{-6}~ A+\frac{6 ~ V}{270000~ \Omega}} ~ \approx ~ 2839~ hours$$
- Where: $$I ~= I_{DDS} + I_{CC} + I_{voltage~divider}$$
- Idds is zero gate voltage drain current. Icc is current consumption of the voltage supervisor.
- Using this approximation we get that it would take over 100 days for the cells to hit 2.5 V. Using better 18650 cells that have 0.5 Ah capacity left at 3 V the time would be extended to almost 600 days.
- This is the circuit I have decided to use:
- 
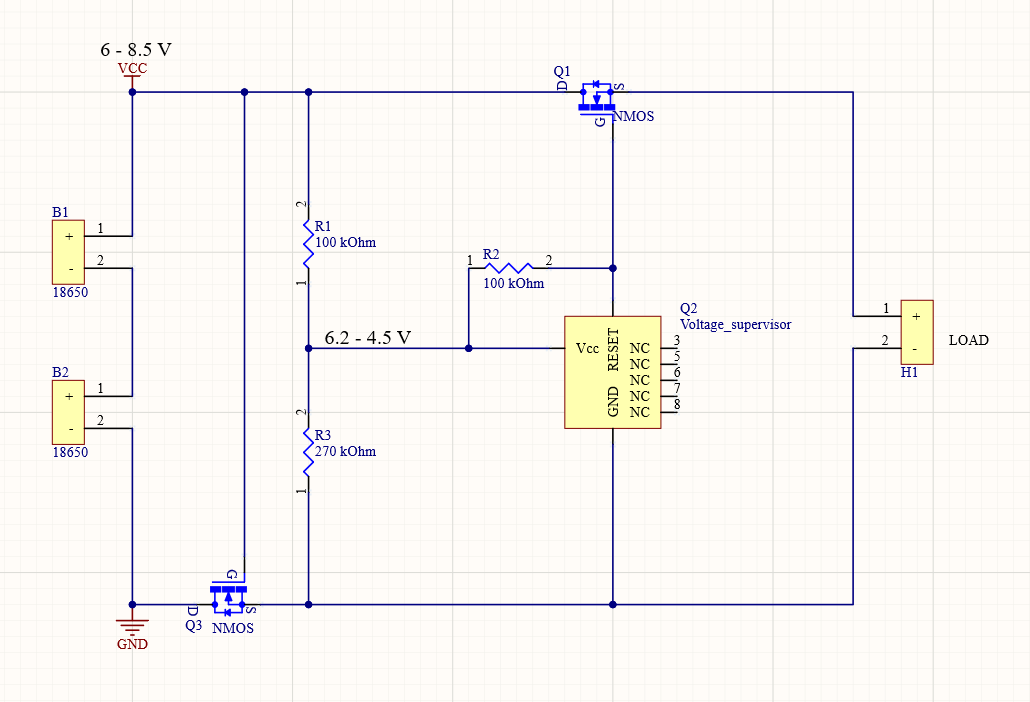
- The cut-off voltage will be just above 6 V. MOSFETs used are [SiRA14BDP](https://www.vishay.com/docs/76789/sira14bdp.pdf) and the voltage supervisor is [TS831](https://www.st.com/en/reset-and-supervisor-ics/ts831.html). Maximum current consumption of TS831 is just 12 uA.
- For the voltage on one cell to hit dangerous level it needs to drop from 3 V to 2.5 V. From discharge rate characteristics of any 18650 cell we can get its capacity in voltage range 3 - 2.5 V. It will be anywhere from 0.1 Ah to 0.5 Ah. If we assume the worst case, the approximation for how long it will take for the cell to hit dangerous level is:
- $$Time = \frac{Capacity}{I} = \frac{0.1 ~ Ah}{1\cdot 10^{-6} ~ A+12\cdot 10^{-6}~ A+\frac{6 ~ V}{270000~ \Omega}} ~ \approx ~ 2839~ hours$$
- Where: $$I ~= I_{DDS} + I_{CC} + I_{voltage~divider}$$
- Idds is zero gate voltage drain current. Icc is current consumption of the voltage supervisor.
- Using this approximation we get that it would take over 100 days for the cells to hit 2.5 V. Using better 18650 cells that have 0.5 Ah capacity left at 3 V the time would be extended to almost 600 days.
#1: Initial revision
by
Stefan
·
2022-08-01T20:18:53Z (over 1 year ago)
This is the circuit I have decided to use:
The cut-off voltage will be just above 6 V. MOSFETs used are [SiRA14BDP](https://www.vishay.com/docs/76789/sira14bdp.pdf) and the voltage supervisor is [TS831](https://www.st.com/en/reset-and-supervisor-ics/ts831.html). Maximum current consumption of TS831 is just 12 uA.
For the voltage on one cell to hit dangerous level it needs to drop from 3 V to 2.5 V. From discharge rate characteristics of any 18650 cell we can get its capacity in voltage range 3 - 2.5 V. It will be anywhere from 0.1 Ah to 0.5 Ah. If we assume the worst case, the approximation for how long it will take for the cell to hit dangerous level is:
$$Time = \frac{Capacity}{I} = \frac{0.1 ~ Ah}{1\cdot 10^{-6} ~ A+12\cdot 10^{-6}~ A+\frac{6 ~ V}{270000~ \Omega}} ~ \approx ~ 2839~ hours$$
Where: $$I ~= I_{DDS} + I_{CC} + I_{voltage~divider}$$
Idds is zero gate voltage drain current. Icc is current consumption of the voltage supervisor.
Using this approximation we get that it would take over 100 days for the cells to hit 2.5 V. Using better 18650 cells that have 0.5 Ah capacity left at 3 V the time would be extended to almost 600 days.