Post History
You still haven't said why you need, or even what order, type, etc. Assuming it's a 2nd order, an exact solution involves creating a generic transfer function and then solving a system of equations...
Answer
#1: Initial revision
by
a concerned citizen
·
2022-08-14T08:03:30Z (over 1 year ago)
You still haven't said why you need, or even what order, type, etc. Assuming it's a 2nd order, an exact solution involves creating a generic transfer function and then solving a system of equations with imposed conditions (use squared to get rid of radical):
$$\begin{align}
H(s)&=\dfrac{s^2}{s^2+as+b} \tag{1} \\\\
&\begin{cases}
|H(j)|^2&=\dfrac12 \\\\
|H(j/2)|^2&=\left(10^{-8/20}\right)^2
\end{cases}
\end{align}$$
You wil get four solutions (4 combinations):
$$\begin{cases}
a_{1,2,3,4}&=[+,-,-,+]0.33035 \\\\
b_{1,2,3,4}&=[+,+,-,-]0.47976
\end{cases} \tag{2}$$
Since the denominator needs to be a [Hurwitz polynomial](https://en.wikipedia.org/wiki/Hurwitz_polynomial) only the positive values are chosen (the 1st pair), which results in a perfect match:
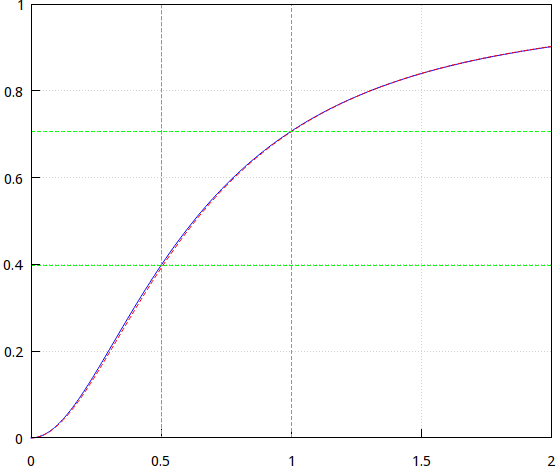
$$\begin{align}
|H(j)|&=0.70711\space(0.70597) \\\\
|H(j0.5)|&=0.39811\space(0.39165)
\end{align}$$
In parenthesis are the results of [@TonyStewart's solution](https://electrical.codidact.com/posts/286730/286867#answer-286867), tweaked to have $f=0.42\space(2f=0.84)$. And these are the plots (Tony's is dashed):
