Post History
Yeah, that looks like it's going to be messy. I agree with Olin: the problem starts with three variables and three conditions so, no matter how you look at it, you will end up with a system of...
#6: Post edited
- > Yeah, that looks like it's going to be messy.
- I agree with Olin: the problem starts with three variables and three conditions so, no matter how you look at it, you will end up with a system of equations.
- However, you can take certain shortcuts (using your 1st picture):
- $$\begin{align}
- R_{23}&=R_3||(R_2+R_o) \tag{1} \\
- R_{13}&=R_3||(R_1+R_i) \tag{2} \\
- R_i&=R_1+R_{23} \tag{3} \\
- R_o&=R_2+R_{13} \tag{4}
- \end{align}$$
- [edit]
- [edit 2]
- $R_{23}$ is the resistance at point X with the input disconnected, and $R_{13}$ is the rsistance at point X with the output disconnected.
- Then, the input source always sees its $R_i$ in series with the equivalent $R_i$, while the output voltage is always $\frac{A}2$ over $R_o||R_o^{eq}$ ($A$ is the attenuation relative to a unity input). Thus:
- $$\begin{align}
- I_1&=\dfrac{1}{2R_i} \tag{5} \\
- I_2&=\dfrac{A}{2R_o} \tag{6} \\
- I_3&=I_1-I_2=\dfrac12\left(\dfrac{1}{R_i}-\dfrac{A}{R_o}\right) \tag{7}
- \end{align}$$
- Since the biggest unknown is $V_x$, calculate it with (3) in mind:
- Now calculate $R_2$ and $R_3$ based on (6), (7), and (8), while considering that $V_1=\frac12$ and $V_2=\frac{A}{2}$:
- $$\begin{align}
- R_2&=\dfrac{V_x-V_2}{I_2}=\left(\dfrac{2V_x}{A}-1\right)R_o=\left(\dfrac{1-\dfrac{R_1}{R_i}}{A}-1\right)R_o=\dfrac{\big((1-A)R_i-R_1\big)R_o}{AR_i} \tag{9} \\
- R_3&=\dfrac{V_1-V_x}{I_1}=\dfrac{2V_xR_iR_o}{R_o-AR_i}=\dfrac{\left(1-\dfrac{R_1}{R_i}\right)R_iR_o}{R_o-AR_i}=\dfrac{(R_i-R_1)R_o}{R_o-AR_i} \tag{10}
- \end{align}$$
- Since $R_i$, $A$, and $R_o$ are given, both (9) and (10) are dependent on $R_1$, only. Now, use (2) and (4) to derive the expression for $R_1$:
- After expanding and collecting the terms:
- Substituting (9) and (10) in (12) takes a few lines of simplifications to give:
- At this point, if you want to keep things simple(-ish) then use $(\text{I})$ for $R_1$ and then, sequentially, calculate (9) and (10) through substitution. Otherwise, you'll need a few more lines of simplifications to give:
- $$\begin{align}
- R_2&=\dfrac{R_o^2+(A^2-2A)R_iR_o}{R_o-A^2R_i} \tag{II} \\
- R_3&=\dfrac{2AR_iR_o}{R_o-A^2R_i} \tag{III} \\
- \end{align}$$
- I find it interesting that all of them are divided by $R_o-A^2R_i$. Maybe there is something to it, hopefully a simplification but, now, my eyes are getting crossed by the amount of MathJax so, I'll take a break. I'll double check later on but, for now, it looks like I haven't made any mistakes.
- A SPICE test with your values confirms both approaches (blue text is active, upper sources output the resistor values, `k` means $A$):
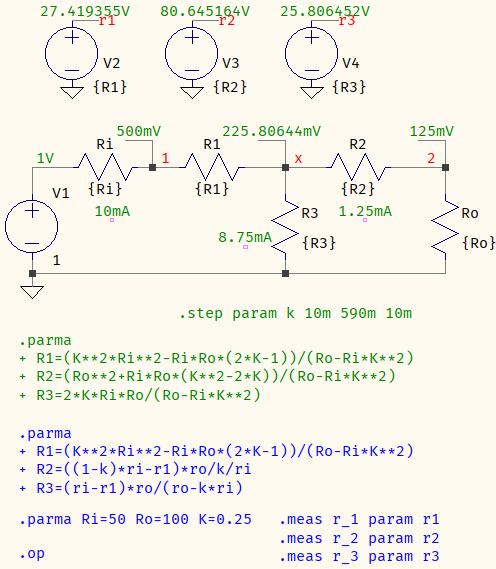
- > Yeah, that looks like it's going to be messy.
- I agree with Olin: the problem starts with three variables and three conditions so, no matter how you look at it, you will end up with a system of equations.
- However, you can take certain shortcuts (using your 1st picture):
- $$\begin{align}
- R_{23}&=R_3||(R_2+R_o) \tag{1} \\
- R_{13}&=R_3||(R_1+R_i) \tag{2} \\
- R_i&=R_1+R_{23} \tag{3} \\
- R_o&=R_2+R_{13} \tag{4}
- \end{align}$$
- [edit]
- [edit 2]
- $R_{23}$ is the resistance at point X with the input disconnected, and $R_{13}$ is the rsistance at point X with the output disconnected.
- Then, the input source always sees its $R_i$ in series with the equivalent $R_i$, while the output voltage is always $\frac{A}2$ over $R_o||R_o^{eq}$ ($A$ is the attenuation relative to a unity input). Thus:
- $$\begin{align}
- I_1&=\dfrac{1}{2R_i} \tag{5} \\
- I_2&=\dfrac{A}{2R_o} \tag{6} \\
- I_3&=I_1-I_2=\dfrac12\left(\dfrac{1}{R_i}-\dfrac{A}{R_o}\right) \tag{7}
- \end{align}$$
- Since the biggest unknown is $V_x$, calculate it with (3) in mind:
- Now calculate $R_2$ and $R_3$ based on (6), (7), and (8), while considering that $V_1=\frac12$ and $V_2=\frac{A}{2}$:
- $$\begin{align}
- R_2&=\dfrac{V_x-V_2}{I_2}=\left(\dfrac{2V_x}{A}-1\right)R_o=\left(\dfrac{1-\dfrac{R_1}{R_i}}{A}-1\right)R_o=\dfrac{\big((1-A)R_i-R_1\big)R_o}{AR_i} \tag{9} \\
- R_3&=\dfrac{V_1-V_x}{I_1}=\dfrac{2V_xR_iR_o}{R_o-AR_i}=\dfrac{\left(1-\dfrac{R_1}{R_i}\right)R_iR_o}{R_o-AR_i}=\dfrac{(R_i-R_1)R_o}{R_o-AR_i} \tag{10}
- \end{align}$$
- Since $R_i$, $A$, and $R_o$ are given, both (9) and (10) are dependent on $R_1$, only. Now, use (2) and (4) to derive the expression for $R_1$:
- After expanding and collecting the terms:
- Substituting (9) and (10) in (12) takes a few lines of simplifications to give:
- At this point, if you want to keep things simple(-ish) then use $(\text{I})$ for $R_1$ and then, sequentially, calculate (9) and (10) through substitution. Otherwise, you'll need a few more lines of simplifications to give:
- $$\begin{align}
- R_2&=\dfrac{R_o^2+(A^2-2A)R_iR_o}{R_o-A^2R_i} \tag{II} \\
- R_3&=\dfrac{2AR_iR_o}{R_o-A^2R_i} \tag{III} \\
- \end{align}$$
- I find it interesting that all of them are divided by $R_o-A^2R_i$. Maybe there is something to it, hopefully a simplification but, now, my eyes are getting crossed by the amount of MathJax so, I'll take a break. I'll double check later on but, for now, it looks like I haven't made any mistakes.
- A SPICE test with your values confirms both approaches (blue text is active, upper sources output the resistor values, `k` means $A$):
- 
- ---
- [edit 3]
- This is mostly cosmetic, it certainly doesn't reduce the derivation (it actually adds to it) but, inspired by the formulas from [this site](https://circuitsgeek.com/tutorials/t-pad-attenuator/) (which do not account for correct attenuation), $R_3$ can be calculated as in ($\text{III}$) and then $R_1$ and $R_2$ calculated from (3) and (4), based on it, resulting in slightly more palatable equations:
- $$\begin{align}
- R_1&=\sqrt{\dfrac{\bbox[5px,border:black solid 1px]{R_i}}{R_o}}\sqrt{R_iR_o+R_3^2}-R_3 \tag{IV} \\
- R_2&=\sqrt{\dfrac{R_o}{\bbox[5px,border:black solid 1px]{R_i}}}\sqrt{R_iR_o+R_3^2}-R_3 \tag{V}
- \end{align}$$
#5: Post edited
- > Yeah, that looks like it's going to be messy.
- I agree with Olin: the problem starts with three variables and three conditions so, no matter how you look at it, you will end up with a system of equations.
- However, you can take certain shortcuts (using your 1st picture):
- $$\begin{align}
- R_{23}&=R_3||(R_2+R_o) \tag{1} \\
- R_{13}&=R_3||(R_1+R_i) \tag{2} \\
- R_i&=R_1+R_{23} \tag{3} \\
- R_o&=R_2+R_{13} \tag{4}
- \end{align}$$
- [edit]
$R_{23}$ is the resistance at point X seen from the input, and $R_{13}$ is the rsistance at point X seen from the output.- Then, the input source always sees its $R_i$ in series with the equivalent $R_i$, while the output voltage is always $\frac{A}2$ over $R_o||R_o^{eq}$ ($A$ is the attenuation relative to a unity input). Thus:
- $$\begin{align}
- I_1&=\dfrac{1}{2R_i} \tag{5} \\
- I_2&=\dfrac{A}{2R_o} \tag{6} \\
- I_3&=I_1-I_2=\dfrac12\left(\dfrac{1}{R_i}-\dfrac{A}{R_o}\right) \tag{7}
- \end{align}$$
- Since the biggest unknown is $V_x$, calculate it with (3) in mind:
- Now calculate $R_2$ and $R_3$ based on (6), (7), and (8), while considering that $V_1=\frac12$ and $V_2=\frac{A}{2}$:
- $$\begin{align}
- R_2&=\dfrac{V_x-V_2}{I_2}=\left(\dfrac{2V_x}{A}-1\right)R_o=\left(\dfrac{1-\dfrac{R_1}{R_i}}{A}-1\right)R_o=\dfrac{\big((1-A)R_i-R_1\big)R_o}{AR_i} \tag{9} \\
- R_3&=\dfrac{V_1-V_x}{I_1}=\dfrac{2V_xR_iR_o}{R_o-AR_i}=\dfrac{\left(1-\dfrac{R_1}{R_i}\right)R_iR_o}{R_o-AR_i}=\dfrac{(R_i-R_1)R_o}{R_o-AR_i} \tag{10}
- \end{align}$$
- Since $R_i$, $A$, and $R_o$ are given, both (9) and (10) are dependent on $R_1$, only. Now, use (2) and (4) to derive the expression for $R_1$:
- After expanding and collecting the terms:
- Substituting (9) and (10) in (12) takes a few lines of simplifications to give:
- At this point, if you want to keep things simple(-ish) then use $(\text{I})$ for $R_1$ and then, sequentially, calculate (9) and (10) through substitution. Otherwise, you'll need a few more lines of simplifications to give:
- $$\begin{align}
- R_2&=\dfrac{R_o^2+(A^2-2A)R_iR_o}{R_o-A^2R_i} \tag{II} \\
- R_3&=\dfrac{2AR_iR_o}{R_o-A^2R_i} \tag{III} \\
- \end{align}$$
- I find it interesting that all of them are divided by $R_o-A^2R_i$. Maybe there is something to it, hopefully a simplification but, now, my eyes are getting crossed by the amount of MathJax so, I'll take a break. I'll double check later on but, for now, it looks like I haven't made any mistakes.
- A SPICE test with your values confirms both approaches (blue text is active, upper sources output the resistor values, `k` means $A$):
- 
- > Yeah, that looks like it's going to be messy.
- I agree with Olin: the problem starts with three variables and three conditions so, no matter how you look at it, you will end up with a system of equations.
- However, you can take certain shortcuts (using your 1st picture):
- $$\begin{align}
- R_{23}&=R_3||(R_2+R_o) \tag{1} \\
- R_{13}&=R_3||(R_1+R_i) \tag{2} \\
- R_i&=R_1+R_{23} \tag{3} \\
- R_o&=R_2+R_{13} \tag{4}
- \end{align}$$
- [edit]
- [edit 2]
- $R_{23}$ is the resistance at point X with the input disconnected, and $R_{13}$ is the rsistance at point X with the output disconnected.
- Then, the input source always sees its $R_i$ in series with the equivalent $R_i$, while the output voltage is always $\frac{A}2$ over $R_o||R_o^{eq}$ ($A$ is the attenuation relative to a unity input). Thus:
- $$\begin{align}
- I_1&=\dfrac{1}{2R_i} \tag{5} \\
- I_2&=\dfrac{A}{2R_o} \tag{6} \\
- I_3&=I_1-I_2=\dfrac12\left(\dfrac{1}{R_i}-\dfrac{A}{R_o}\right) \tag{7}
- \end{align}$$
- Since the biggest unknown is $V_x$, calculate it with (3) in mind:
- Now calculate $R_2$ and $R_3$ based on (6), (7), and (8), while considering that $V_1=\frac12$ and $V_2=\frac{A}{2}$:
- $$\begin{align}
- R_2&=\dfrac{V_x-V_2}{I_2}=\left(\dfrac{2V_x}{A}-1\right)R_o=\left(\dfrac{1-\dfrac{R_1}{R_i}}{A}-1\right)R_o=\dfrac{\big((1-A)R_i-R_1\big)R_o}{AR_i} \tag{9} \\
- R_3&=\dfrac{V_1-V_x}{I_1}=\dfrac{2V_xR_iR_o}{R_o-AR_i}=\dfrac{\left(1-\dfrac{R_1}{R_i}\right)R_iR_o}{R_o-AR_i}=\dfrac{(R_i-R_1)R_o}{R_o-AR_i} \tag{10}
- \end{align}$$
- Since $R_i$, $A$, and $R_o$ are given, both (9) and (10) are dependent on $R_1$, only. Now, use (2) and (4) to derive the expression for $R_1$:
- After expanding and collecting the terms:
- Substituting (9) and (10) in (12) takes a few lines of simplifications to give:
- At this point, if you want to keep things simple(-ish) then use $(\text{I})$ for $R_1$ and then, sequentially, calculate (9) and (10) through substitution. Otherwise, you'll need a few more lines of simplifications to give:
- $$\begin{align}
- R_2&=\dfrac{R_o^2+(A^2-2A)R_iR_o}{R_o-A^2R_i} \tag{II} \\
- R_3&=\dfrac{2AR_iR_o}{R_o-A^2R_i} \tag{III} \\
- \end{align}$$
- I find it interesting that all of them are divided by $R_o-A^2R_i$. Maybe there is something to it, hopefully a simplification but, now, my eyes are getting crossed by the amount of MathJax so, I'll take a break. I'll double check later on but, for now, it looks like I haven't made any mistakes.
- A SPICE test with your values confirms both approaches (blue text is active, upper sources output the resistor values, `k` means $A$):
- 
#4: Post edited
- > Yeah, that looks like it's going to be messy.
- I agree with Olin: the problem starts with three variables and three conditions so, no matter how you look at it, you will end up with a system of equations.
- However, you can take certain shortcuts (using your 1st picture):
- $$\begin{align}
- R_{23}&=R_3||(R_2+R_o) \tag{1} \\
- R_{13}&=R_3||(R_1+R_i) \tag{2} \\
- R_i&=R_1+R_{23} \tag{3} \\
- R_o&=R_2+R_{13} \tag{4}
- \end{align}$$
- [edit]
- $R_{23}$ is the resistance at point X seen from the input, and $R_{13}$ is the rsistance at point X seen from the output.
- Then, the input source always sees its $R_i$ in series with the equivalent $R_i$, while the output voltage is always $\frac{A}2$ over $R_o||R_o^{eq}$ ($A$ is the attenuation relative to a unity input). Thus:
- $$\begin{align}
- I_1&=\dfrac{1}{2R_i} \tag{5} \\
- I_2&=\dfrac{A}{2R_o} \tag{6} \\
- I_3&=I_1-I_2=\dfrac12\left(\dfrac{1}{R_i}-\dfrac{A}{R_o}\right) \tag{7}
- \end{align}$$
- Since the biggest unknown is $V_x$, calculate it with (3) in mind:
Now calculate $R_2$ and $R_3$ based on (6), (7), and (8):- $$\begin{align}
- R_2&=\dfrac{V_x-V_2}{I_2}=\left(\dfrac{2V_x}{A}-1\right)R_o=\left(\dfrac{1-\dfrac{R_1}{R_i}}{A}-1\right)R_o=\dfrac{\big((1-A)R_i-R_1\big)R_o}{AR_i} \tag{9} \\
- R_3&=\dfrac{V_1-V_x}{I_1}=\dfrac{2V_xR_iR_o}{R_o-AR_i}=\dfrac{\left(1-\dfrac{R_1}{R_i}\right)R_iR_o}{R_o-AR_i}=\dfrac{(R_i-R_1)R_o}{R_o-AR_i} \tag{10}
- \end{align}$$
- Since $R_i$, $A$, and $R_o$ are given, both (9) and (10) are dependent on $R_1$, only. Now, use (2) and (4) to derive the expression for $R_1$:
- After expanding and collecting the terms:
- Substituting (9) and (10) in (12) takes a few lines of simplifications to give:
- At this point, if you want to keep things simple(-ish) then use $(\text{I})$ for $R_1$ and then, sequentially, calculate (9) and (10) through substitution. Otherwise, you'll need a few more lines of simplifications to give:
- $$\begin{align}
- R_2&=\dfrac{R_o^2+(A^2-2A)R_iR_o}{R_o-A^2R_i} \tag{II} \\
- R_3&=\dfrac{2AR_iR_o}{R_o-A^2R_i} \tag{III} \\
- \end{align}$$
- I find it interesting that all of them are divided by $R_o-A^2R_i$. Maybe there is something to it, hopefully a simplification but, now, my eyes are getting crossed by the amount of MathJax so, I'll take a break. I'll double check later on but, for now, it looks like I haven't made any mistakes.
- A SPICE test with your values confirms both approaches (blue text is active, upper sources output the resistor values, `k` means $A$):
- 
- > Yeah, that looks like it's going to be messy.
- I agree with Olin: the problem starts with three variables and three conditions so, no matter how you look at it, you will end up with a system of equations.
- However, you can take certain shortcuts (using your 1st picture):
- $$\begin{align}
- R_{23}&=R_3||(R_2+R_o) \tag{1} \\
- R_{13}&=R_3||(R_1+R_i) \tag{2} \\
- R_i&=R_1+R_{23} \tag{3} \\
- R_o&=R_2+R_{13} \tag{4}
- \end{align}$$
- [edit]
- $R_{23}$ is the resistance at point X seen from the input, and $R_{13}$ is the rsistance at point X seen from the output.
- Then, the input source always sees its $R_i$ in series with the equivalent $R_i$, while the output voltage is always $\frac{A}2$ over $R_o||R_o^{eq}$ ($A$ is the attenuation relative to a unity input). Thus:
- $$\begin{align}
- I_1&=\dfrac{1}{2R_i} \tag{5} \\
- I_2&=\dfrac{A}{2R_o} \tag{6} \\
- I_3&=I_1-I_2=\dfrac12\left(\dfrac{1}{R_i}-\dfrac{A}{R_o}\right) \tag{7}
- \end{align}$$
- Since the biggest unknown is $V_x$, calculate it with (3) in mind:
- Now calculate $R_2$ and $R_3$ based on (6), (7), and (8), while considering that $V_1=\frac12$ and $V_2=\frac{A}{2}$:
- $$\begin{align}
- R_2&=\dfrac{V_x-V_2}{I_2}=\left(\dfrac{2V_x}{A}-1\right)R_o=\left(\dfrac{1-\dfrac{R_1}{R_i}}{A}-1\right)R_o=\dfrac{\big((1-A)R_i-R_1\big)R_o}{AR_i} \tag{9} \\
- R_3&=\dfrac{V_1-V_x}{I_1}=\dfrac{2V_xR_iR_o}{R_o-AR_i}=\dfrac{\left(1-\dfrac{R_1}{R_i}\right)R_iR_o}{R_o-AR_i}=\dfrac{(R_i-R_1)R_o}{R_o-AR_i} \tag{10}
- \end{align}$$
- Since $R_i$, $A$, and $R_o$ are given, both (9) and (10) are dependent on $R_1$, only. Now, use (2) and (4) to derive the expression for $R_1$:
- After expanding and collecting the terms:
- Substituting (9) and (10) in (12) takes a few lines of simplifications to give:
- At this point, if you want to keep things simple(-ish) then use $(\text{I})$ for $R_1$ and then, sequentially, calculate (9) and (10) through substitution. Otherwise, you'll need a few more lines of simplifications to give:
- $$\begin{align}
- R_2&=\dfrac{R_o^2+(A^2-2A)R_iR_o}{R_o-A^2R_i} \tag{II} \\
- R_3&=\dfrac{2AR_iR_o}{R_o-A^2R_i} \tag{III} \\
- \end{align}$$
- I find it interesting that all of them are divided by $R_o-A^2R_i$. Maybe there is something to it, hopefully a simplification but, now, my eyes are getting crossed by the amount of MathJax so, I'll take a break. I'll double check later on but, for now, it looks like I haven't made any mistakes.
- A SPICE test with your values confirms both approaches (blue text is active, upper sources output the resistor values, `k` means $A$):
- 
#3: Post edited
- > Yeah, that looks like it's going to be messy.
- I agree with Olin: the problem starts with three variables and three conditions so, no matter how you look at it, you will end up with a system of equations.
- However, you can take certain shortcuts (using your 1st picture):
- $$\begin{align}
- R_{23}&=R_3||(R_2+R_o) \tag{1} \\
- R_{13}&=R_3||(R_1+R_i) \tag{2} \\
- R_i&=R_1+R_{23} \tag{3} \\
- R_o&=R_2+R_{13} \tag{4}
- \end{align}$$
Then, the input source always sees its $R_i$ in series with the equivalent $R_i$, while the output voltage is always $\frac{k}2$ over $R_o||R_o^{eq}$, thus:- $$\begin{align}
- I_1&=\dfrac{1}{2R_i} \tag{5} \\
I_2&=\dfrac{k}{2R_o} \tag{6} \\I_3&=I_1-I_2=\dfrac12\left(\dfrac{1}{R_i}-\dfrac{k}{R_o} ight) \tag{7}- \end{align}$$
- Since the biggest unknown is $V_x$, calculate it with (3) in mind:
- Now calculate $R_2$ and $R_3$ based on (6), (7), and (8):
- $$\begin{align}
R_2&=\dfrac{V_x-\dfrac{k}{2}}{\dfrac{1}{2R_i}}=\left(\dfrac{2V_x}{k}-1 ight)R_o=\left(\dfrac{1-\dfrac{R_1}{R_i}}{k}-1 ight)R_o=\dfrac{\big((1-k)R_i-R_1\big)R_o}{kR_i} \tag{9} \\R_3&=\dfrac{V_x}{\dfrac12\left(\dfrac{1}{R_i}-\dfrac{k}{R_o}\right)}=\dfrac{2V_xR_iR_o}{R_o-kR_i}=\dfrac{\left(1-\dfrac{R_1}{R_i} ight)R_iR_o}{R_o-kR_i}=\dfrac{(R_i-R_1)R_o}{R_o-kR_i} \tag{10}- \end{align}$$
Since $R_i$, $k$, and $R_o$ are given, both (9) and (10) are dependent on $R_1$, only. Now, use (2) and (4) to derive the expression for $R_1$:- After expanding and collecting the terms:
- Substituting (9) and (10) in (12) takes a few lines of simplifications to give:
$$R_1=\dfrac{k^2R_i^2-(2k-1)R_i^2R_o}{R_o-k^2R_i} \tag{I}$$- At this point, if you want to keep things simple(-ish) then use $(\text{I})$ for $R_1$ and then, sequentially, calculate (9) and (10) through substitution. Otherwise, you'll need a few more lines of simplifications to give:
- $$\begin{align}
R_2&=\dfrac{R_o^2+(k^2-2k)R_iR_o}{R_o-k^2R_i} \tag{II} \\R_3&=\dfrac{2kR_iR_o}{R_o-k^2R_i} \tag{III} \\- \end{align}$$
I find it interesting that all of them are divided by $R_o-k^2R_i$. Maybe there is something to it, hopefully a simplification but, now, my eyes are getting crossed by the amount of MathJax so, I'll take a break. I'll double check later on but, for now, it looks like I haven't made any mistakes.A SPICE test with your values confirms both approaches (blue text is active, upper sources output the resistor values):- 
- > Yeah, that looks like it's going to be messy.
- I agree with Olin: the problem starts with three variables and three conditions so, no matter how you look at it, you will end up with a system of equations.
- However, you can take certain shortcuts (using your 1st picture):
- $$\begin{align}
- R_{23}&=R_3||(R_2+R_o) \tag{1} \\
- R_{13}&=R_3||(R_1+R_i) \tag{2} \\
- R_i&=R_1+R_{23} \tag{3} \\
- R_o&=R_2+R_{13} \tag{4}
- \end{align}$$
- [edit]
- $R_{23}$ is the resistance at point X seen from the input, and $R_{13}$ is the rsistance at point X seen from the output.
- Then, the input source always sees its $R_i$ in series with the equivalent $R_i$, while the output voltage is always $\frac{A}2$ over $R_o||R_o^{eq}$ ($A$ is the attenuation relative to a unity input). Thus:
- $$\begin{align}
- I_1&=\dfrac{1}{2R_i} \tag{5} \\
- I_2&=\dfrac{A}{2R_o} \tag{6} \\
- I_3&=I_1-I_2=\dfrac12\left(\dfrac{1}{R_i}-\dfrac{A}{R_o} ight) \tag{7}
- \end{align}$$
- Since the biggest unknown is $V_x$, calculate it with (3) in mind:
- Now calculate $R_2$ and $R_3$ based on (6), (7), and (8):
- $$\begin{align}
- R_2&=\dfrac{V_x-V_2}{I_2}=\left(\dfrac{2V_x}{A}-1 ight)R_o=\left(\dfrac{1-\dfrac{R_1}{R_i}}{A}-1 ight)R_o=\dfrac{\big((1-A)R_i-R_1\big)R_o}{AR_i} \tag{9} \\
- R_3&=\dfrac{V_1-V_x}{I_1}=\dfrac{2V_xR_iR_o}{R_o-AR_i}=\dfrac{\left(1-\dfrac{R_1}{R_i} ight)R_iR_o}{R_o-AR_i}=\dfrac{(R_i-R_1)R_o}{R_o-AR_i} \tag{10}
- \end{align}$$
- Since $R_i$, $A$, and $R_o$ are given, both (9) and (10) are dependent on $R_1$, only. Now, use (2) and (4) to derive the expression for $R_1$:
- After expanding and collecting the terms:
- Substituting (9) and (10) in (12) takes a few lines of simplifications to give:
- $$R_1=\dfrac{R_i^2\big(A^2-(2A-1)R_o\big)}{R_o-A^2R_i} \tag{I}$$
- At this point, if you want to keep things simple(-ish) then use $(\text{I})$ for $R_1$ and then, sequentially, calculate (9) and (10) through substitution. Otherwise, you'll need a few more lines of simplifications to give:
- $$\begin{align}
- R_2&=\dfrac{R_o^2+(A^2-2A)R_iR_o}{R_o-A^2R_i} \tag{II} \\
- R_3&=\dfrac{2AR_iR_o}{R_o-A^2R_i} \tag{III} \\
- \end{align}$$
- I find it interesting that all of them are divided by $R_o-A^2R_i$. Maybe there is something to it, hopefully a simplification but, now, my eyes are getting crossed by the amount of MathJax so, I'll take a break. I'll double check later on but, for now, it looks like I haven't made any mistakes.
- A SPICE test with your values confirms both approaches (blue text is active, upper sources output the resistor values, `k` means $A$):
- 
#2: Post edited
- > Yeah, that looks like it's going to be messy.
- I agree with Olin: the problem starts with three variables and three conditions so, no matter how you look at it, you will end up with a system of equations.
- However, you can take certain shortcuts (using your 1st picture):
- $$\begin{align}
- R_{23}&=R_3||(R_2+R_o) \tag{1} \\
- R_{13}&=R_3||(R_1+R_i) \tag{2} \\
- R_i&=R_1+R_{23} \tag{3} \\
- R_o&=R_2+R_{13} \tag{4}
- \end{align}$$
Then, the input source always sees its $R_i$ is series with the equivalent $R_i$, while the output voltage is always $\frac{k}2$ over $R_o||R_o^{eq}$, thus:- $$\begin{align}
- I_1&=\dfrac{1}{2R_i} \tag{5} \\
- I_2&=\dfrac{k}{2R_o} \tag{6} \\
- I_3&=I_1-I_2=\dfrac12\left(\dfrac{1}{R_i}-\dfrac{k}{R_o}\right) \tag{7}
- \end{align}$$
- Since the biggest unknown is $V_x$, calculate it with (3) in mind:
Now calculate $R_2$ and $R_3$ based on (6) and (7):- $$\begin{align}
- R_2&=\dfrac{V_x-\dfrac{k}{2}}{\dfrac{1}{2R_i}}=\left(\dfrac{2V_x}{k}-1\right)R_o=\left(\dfrac{1-\dfrac{R_1}{R_i}}{k}-1\right)R_o=\dfrac{\big((1-k)R_i-R_1\big)R_o}{kR_i} \tag{9} \\
- R_3&=\dfrac{V_x}{\dfrac12\left(\dfrac{1}{R_i}-\dfrac{k}{R_o}\right)}=\dfrac{2V_xR_iR_o}{R_o-kR_i}=\dfrac{\left(1-\dfrac{R_1}{R_i}\right)R_iR_o}{R_o-kR_i}=\dfrac{(R_i-R_1)R_o}{R_o-kR_i} \tag{10}
- \end{align}$$
- Since $R_i$, $k$, and $R_o$ are given, both (9) and (10) are dependent on $R_1$, only. Now, use (2) and (4) to derive the expression for $R_1$:
- After expanding and collecting the terms:
- Substituting (9) and (10) in (12) takes a few lines of simplifications to give:
At this point, if you want to keep things simple(-ish) then use (13) for $R_1$ and then, sequentially, calculate (9) and (10) through substitution. Otherwise, you'll need a few more lines of simplifications to give:- $$\begin{align}
- R_2&=\dfrac{R_o^2+(k^2-2k)R_iR_o}{R_o-k^2R_i} \tag{II} \\
- R_3&=\dfrac{2kR_iR_o}{R_o-k^2R_i} \tag{III} \\
- \end{align}$$
- I find it interesting that all of them are divided by $R_o-k^2R_i$. Maybe there is something to it, hopefully a simplification but, now, my eyes are getting crossed by the amount of MathJax so, I'll take a break. I'll double check later on but, for now, it looks like I haven't made any mistakes.
- A SPICE test with your values confirms both approaches (blue text is active, upper sources output the resistor values):
- 
- > Yeah, that looks like it's going to be messy.
- I agree with Olin: the problem starts with three variables and three conditions so, no matter how you look at it, you will end up with a system of equations.
- However, you can take certain shortcuts (using your 1st picture):
- $$\begin{align}
- R_{23}&=R_3||(R_2+R_o) \tag{1} \\
- R_{13}&=R_3||(R_1+R_i) \tag{2} \\
- R_i&=R_1+R_{23} \tag{3} \\
- R_o&=R_2+R_{13} \tag{4}
- \end{align}$$
- Then, the input source always sees its $R_i$ in series with the equivalent $R_i$, while the output voltage is always $\frac{k}2$ over $R_o||R_o^{eq}$, thus:
- $$\begin{align}
- I_1&=\dfrac{1}{2R_i} \tag{5} \\
- I_2&=\dfrac{k}{2R_o} \tag{6} \\
- I_3&=I_1-I_2=\dfrac12\left(\dfrac{1}{R_i}-\dfrac{k}{R_o}\right) \tag{7}
- \end{align}$$
- Since the biggest unknown is $V_x$, calculate it with (3) in mind:
- Now calculate $R_2$ and $R_3$ based on (6), (7), and (8):
- $$\begin{align}
- R_2&=\dfrac{V_x-\dfrac{k}{2}}{\dfrac{1}{2R_i}}=\left(\dfrac{2V_x}{k}-1\right)R_o=\left(\dfrac{1-\dfrac{R_1}{R_i}}{k}-1\right)R_o=\dfrac{\big((1-k)R_i-R_1\big)R_o}{kR_i} \tag{9} \\
- R_3&=\dfrac{V_x}{\dfrac12\left(\dfrac{1}{R_i}-\dfrac{k}{R_o}\right)}=\dfrac{2V_xR_iR_o}{R_o-kR_i}=\dfrac{\left(1-\dfrac{R_1}{R_i}\right)R_iR_o}{R_o-kR_i}=\dfrac{(R_i-R_1)R_o}{R_o-kR_i} \tag{10}
- \end{align}$$
- Since $R_i$, $k$, and $R_o$ are given, both (9) and (10) are dependent on $R_1$, only. Now, use (2) and (4) to derive the expression for $R_1$:
- After expanding and collecting the terms:
- Substituting (9) and (10) in (12) takes a few lines of simplifications to give:
- At this point, if you want to keep things simple(-ish) then use $(\text{I})$ for $R_1$ and then, sequentially, calculate (9) and (10) through substitution. Otherwise, you'll need a few more lines of simplifications to give:
- $$\begin{align}
- R_2&=\dfrac{R_o^2+(k^2-2k)R_iR_o}{R_o-k^2R_i} \tag{II} \\
- R_3&=\dfrac{2kR_iR_o}{R_o-k^2R_i} \tag{III} \\
- \end{align}$$
- I find it interesting that all of them are divided by $R_o-k^2R_i$. Maybe there is something to it, hopefully a simplification but, now, my eyes are getting crossed by the amount of MathJax so, I'll take a break. I'll double check later on but, for now, it looks like I haven't made any mistakes.
- A SPICE test with your values confirms both approaches (blue text is active, upper sources output the resistor values):
- 
#1: Initial revision
> Yeah, that looks like it's going to be messy.
I agree with Olin: the problem starts with three variables and three conditions so, no matter how you look at it, you will end up with a system of equations.
However, you can take certain shortcuts (using your 1st picture):
$$\begin{align}
R_{23}&=R_3||(R_2+R_o) \tag{1} \\\\
R_{13}&=R_3||(R_1+R_i) \tag{2} \\\\
R_i&=R_1+R_{23} \tag{3} \\\\
R_o&=R_2+R_{13} \tag{4}
\end{align}$$
Then, the input source always sees its \$R_i\$ is series with the equivalent \$R_i\$, while the output voltage is always \$\frac{k}2\$ over \$R_o||R_o^{eq}\$, thus:
$$\begin{align}
I_1&=\dfrac{1}{2R_i} \tag{5} \\\\
I_2&=\dfrac{k}{2R_o} \tag{6} \\\\
I_3&=I_1-I_2=\dfrac12\left(\dfrac{1}{R_i}-\dfrac{k}{R_o}\right) \tag{7}
\end{align}$$
Since the biggest unknown is \$V_x\$, calculate it with (3) in mind:
$$V_x=\dfrac12\dfrac{R_{23}}{R_{23}+R_1}=\dfrac12\dfrac{R_i-R_1}{R_i-R_1+R_1}=\dfrac12\dfrac{R_i-R_1}{R_i}=\dfrac12\left(1-\dfrac{R_1}{R_i}\right) \tag{8}$$
Now calculate \$R_2\$ and \$R_3\$ based on (6) and (7):
$$\begin{align}
R_2&=\dfrac{V_x-\dfrac{k}{2}}{\dfrac{1}{2R_i}}=\left(\dfrac{2V_x}{k}-1\right)R_o=\left(\dfrac{1-\dfrac{R_1}{R_i}}{k}-1\right)R_o=\dfrac{\big((1-k)R_i-R_1\big)R_o}{kR_i} \tag{9} \\\\
R_3&=\dfrac{V_x}{\dfrac12\left(\dfrac{1}{R_i}-\dfrac{k}{R_o}\right)}=\dfrac{2V_xR_iR_o}{R_o-kR_i}=\dfrac{\left(1-\dfrac{R_1}{R_i}\right)R_iR_o}{R_o-kR_i}=\dfrac{(R_i-R_1)R_o}{R_o-kR_i} \tag{10}
\end{align}$$
Since \$R_i\$, \$k\$, and \$R_o\$ are given, both (9) and (10) are dependent on \$R_1\$, only. Now, use (2) and (4) to derive the expression for \$R_1\$:
$$R_o\stackrel{(2,4)}{=}R_2+\dfrac{(R_1+R_i)R_3}{R_1+R_3+R_i} \tag{11}$$
After expanding and collecting the terms:
$$R_1=\dfrac{(R_o-R_2)R_i-(R_2+R_i-R_o)R_3}{R_2+R_3-R_o} \tag{12}$$
Substituting (9) and (10) in (12) takes a few lines of simplifications to give:
$$R_1=\dfrac{k^2R_i^2-(2k-1)R_i^2R_o}{R_o-k^2R_i} \tag{I}$$
At this point, if you want to keep things simple(-ish) then use (13) for \$R_1\$ and then, sequentially, calculate (9) and (10) through substitution. Otherwise, you'll need a few more lines of simplifications to give:
$$\begin{align}
R_2&=\dfrac{R_o^2+(k^2-2k)R_iR_o}{R_o-k^2R_i} \tag{II} \\\\
R_3&=\dfrac{2kR_iR_o}{R_o-k^2R_i} \tag{III} \\\
\end{align}$$
I find it interesting that all of them are divided by \$R_o-k^2R_i\$. Maybe there is something to it, hopefully a simplification but, now, my eyes are getting crossed by the amount of MathJax so, I'll take a break. I'll double check later on but, for now, it looks like I haven't made any mistakes.
A SPICE test with your values confirms both approaches (blue text is active, upper sources output the resistor values):



















