Post History
What is the relationship between the pole zero diagram and bode plot? Case example: a 2nd order RLC low pass filter: - $$\dfrac{V_{OUT}}{V_{IN}} = \dfrac{\frac{1}{j\omega C}}{R+j\omega L +\frac{1}...
#5: Post edited
by
ArtOfCode
·
2020-06-20T11:47:35Z (over 4 years ago)
#4: Post edited
by
ArtOfCode
·
2020-06-20T11:47:26Z (over 4 years ago)
#3: Post edited
by
Andy aka
·
2020-06-19T14:12:14Z (over 4 years ago)
- What is the relationship between the pole zero diagram and bode plot?
- Case example: a 2nd order RLC low pass filter: -
- 
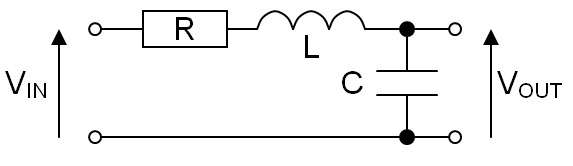
- $$\dfrac{V_{OUT}}{V_{IN}} = \dfrac{\frac{1}{j\omega C}}{R+j\omega L +\frac{1}{j\omega C}} = \dfrac{1}{j\omega RC +j^2\omega^2 LC +1} = \dfrac{\frac{1}{LC}}{\frac{1}{LC}-\omega^2 +j\omega\frac{RC}{LC}}
- $$
Or- $$\dfrac{V_{OUT}}{V_{IN}} =\dfrac{\frac{1}{LC}}{s^2 + s\frac{RC}{LC} + \frac{1}{LC}}
$$
- What is the relationship between the pole zero diagram and bode plot?
- Case example: a 2nd order RLC low pass filter: -
- 
- $$\dfrac{V_{OUT}}{V_{IN}} = \dfrac{\frac{1}{j\omega C}}{R+j\omega L +\frac{1}{j\omega C}} = \dfrac{1}{j\omega RC +j^2\omega^2 LC +1} = \dfrac{\frac{1}{LC}}{\frac{1}{LC}-\omega^2 +j\omega\frac{RC}{LC}}
- $$
- Or, in "s" terms: -
- $$\dfrac{V_{OUT}}{V_{IN}} =\dfrac{\frac{1}{LC}}{s^2 + s\frac{RC}{LC} + \frac{1}{LC}}
- $$
- Therefore we know the poles are defined when the denominator equals zero and: -
- $$s = \dfrac{-R}{2L} ± j\sqrt{\dfrac{1}{LC} - \dfrac{R^2}{4L^2}}$$
- But how does that affect the bode plot?
#2: Post edited
by
Andy aka
·
2020-06-19T11:59:31Z (over 4 years ago)
What is the relationship between the pole zero diagram and bode plot - use the case of a 2nd order RLC low pass filter as an example: -
- What is the relationship between the pole zero diagram and bode plot?
- Case example: a 2nd order RLC low pass filter: -
- 
- $$\dfrac{V_{OUT}}{V_{IN}} = \dfrac{\frac{1}{j\omega C}}{R+j\omega L +\frac{1}{j\omega C}} = \dfrac{1}{j\omega RC +j^2\omega^2 LC +1} = \dfrac{\frac{1}{LC}}{\frac{1}{LC}-\omega^2 +j\omega\frac{RC}{LC}}
- $$
- Or
- $$\dfrac{V_{OUT}}{V_{IN}} =\dfrac{\frac{1}{LC}}{s^2 + s\frac{RC}{LC} + \frac{1}{LC}}
- $$
#1: Initial revision
by
Andy aka
·
2020-06-19T10:45:53Z (over 4 years ago)
What is the relationship between the pole zero diagram and bode plot - use the case of a 2nd order RLC low pass filter as an example: - 