Post History

60%

+1 −0

I find the current flowing through the capacitor $$\begin{align} I_{C_1}(t)&=\dfrac{\mathrm{d}}{\mathrm{d}t}\left[V_1(t)-I_{C_1}(t)R_1\right] \\ {}&= \dfrac{\mathrm{d}}{\mathrm{d}t}\left...

2 answers · posted 3y ago by MissMulan‭ · last activity 3y ago by coquelicot‭

Question voltage current AC

#2: Post edited by

a concerned citizen‭ · 2021-06-18T13:32:06Z (over 3 years ago)
mathjax

Copy Link

Raw

Markdown

Unexpected phase shift in results

I find the current flowing through the capacitor IC1(t)=d/dt(V1(t)-IC1(t)R1)->IC1(t) = d/dt(sint-IC1(t)) and by solving this differential equation we get IC1(t) = (sint+cost-e^-t)/2.To find the voltage of the capacitor we use Ohm's law:Vc1(t) = V1(t)-IC1(t)R1 = sint-cost+e^-t/2.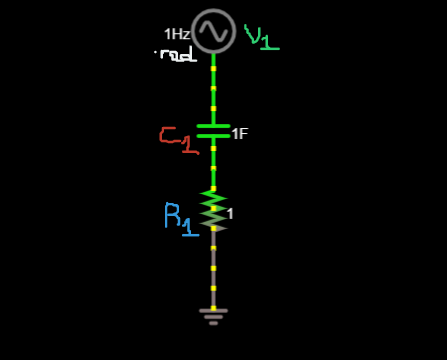
![Check me](https://electrical.codidact.com/uploads/j4PtRhCutfYqdnezEUuktwfH)
But when I plot them on Desmos I get a phase shift of 90 degrees between voltage of the capacitor and current through the capacitor which doesnt make sense it should be 45 degrees what am I doing wrong?

I find the current flowing through the capacitor
$$\begin{align}
I_{C_1}(t)&=\dfrac{\mathrm{d}}{\mathrm{d}t}\left[V_1(t)-I_{C_1}(t)R_1\right] \\\\
{}&= \dfrac{\mathrm{d}}{\mathrm{d}t}\left[\sin(t)-I_{C_1}(t)\right]
\end{align}$$
and by solving this differential equation we get
$$I_{C_1}(t) = \dfrac{\sin(t)+\cos(t)-\mathrm{e}^{-t}}{2}$$
To find the voltage of the capacitor we use Ohm's law:
$$V_{C_1}(t) = V_1(t)-I_{C_1}(t)R_1 = \sin(t)-\cos(t)+\mathrm{e}^{-\frac{t}{2}}$$
![Check me](https://electrical.codidact.com/uploads/j4PtRhCutfYqdnezEUuktwfH)
But when I plot them on Desmos I get a phase shift of 90 degrees between voltage of the capacitor and current through the capacitor which doesnt make sense it should be 45 degrees what am I doing wrong?

voltage current AC

#1: Initial revision by

MissMulan‭ · 2021-06-18T06:47:31Z (over 3 years ago)

Copy Link

Raw

Markdown

Unexpected phase shift in results

I find the current flowing through the capacitor IC1(t)=d/dt(V1(t)-IC1(t)R1)->IC1(t) = d/dt(sint-IC1(t)) and by solving this differential equation we get IC1(t) = (sint+cost-e^-t)/2.To find the voltage of the capacitor we use Ohm's law:Vc1(t) = V1(t)-IC1(t)R1 = sint-cost+e^-t/2.

![Check me](https://electrical.codidact.com/uploads/j4PtRhCutfYqdnezEUuktwfH)

But when I plot them on Desmos I get a phase shift of 90 degrees between voltage of the capacitor and current through the capacitor which doesnt make sense it should be 45 degrees what am I doing wrong?

voltage current AC

Communities

Post History