Post History
I am designing a DC/DC converter in the control loop of which a transconductance amplifier (OTA) is used. This part of circuit looks like this: To determine the needed characteristics, I am usin...
#2: Post edited
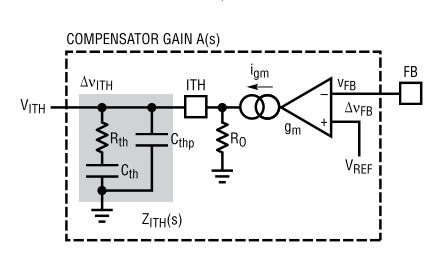
- I am designing a DC/DC converter in the control loop of which a transconductance amplifier (OTA) is used. This part of circuit looks like this:
- 
- To determine the needed characteristics, I am using a transfer function provided by the manufacturer (AD). However, today I decided to check the transfer function by hand and encountered a roadblock.
- The manufacturer (and other sources) say that the transfer function is:
- 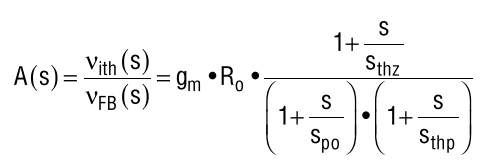
- where:
- * `s_thz = 1/(Rth*Cth)`, zero contributed by the resistor
- * `s_po = 1/(Ro*Cth)`, pole contributed by the op-amp input resistance and `Cth`
* `s_thp = 1/(Ro*Cth)`, high-frequency pole contributed by the `Cthp` capacitor- I could derive the transfer function for the network of `Cth, Rth` and `Cthp` with no issue. I observe the high-frequency pole, a zero and a pole at origin typical of those configurations.
- However, as the [application note discussing compensation networks](https://www.analog.com/media/en/technical-documentation/application-notes/an149fa.pdf) points out, the OTA is not ideal and so its impedance wil move the pole off of the origin. It is still a low- frequency pole, but the 'pole at origin' model becomes inaccurate.
- This is where I encounter my issue. The transfer function provided by the manufacturer is very clean. However, when I add the OTA output impedance, my transfer function grows in size. The poles are no longer a simple fraction, but rather incorporate every component of the compensator.
- This does make sense to me (after all, the OTA impedance 'sees' the whole network and not only one capacitor). Furthermore, the manufacturer also mentions simplifying the transfer function as well.
- However, I cannot find a full derivation of the type II compensator anywhere on the internet. So, keeping the above in mind, my questions are:
- * What is the accurate transfer function for this circuit?
- * Why can we calculate the influence of the output impedance taking only the Cth capacitor into account?
- I would appreciate any help with this question as I have been wrestling with this transfer function for a while now.
- I am designing a DC/DC converter in the control loop of which a transconductance amplifier (OTA) is used. This part of circuit looks like this:
- 
- To determine the needed characteristics, I am using a transfer function provided by the manufacturer (AD). However, today I decided to check the transfer function by hand and encountered a roadblock.
- The manufacturer (and other sources) say that the transfer function is:
- 
- where:
- * `s_thz = 1/(Rth*Cth)`, zero contributed by the resistor
- * `s_po = 1/(Ro*Cth)`, pole contributed by the op-amp input resistance and `Cth`
- * `s_thp = 1/(Rth*Cthp)`, high-frequency pole contributed by the `Cthp` capacitor
- I could derive the transfer function for the network of `Cth, Rth` and `Cthp` with no issue. I observe the high-frequency pole, a zero and a pole at origin typical of those configurations.
- However, as the [application note discussing compensation networks](https://www.analog.com/media/en/technical-documentation/application-notes/an149fa.pdf) points out, the OTA is not ideal and so its impedance wil move the pole off of the origin. It is still a low- frequency pole, but the 'pole at origin' model becomes inaccurate.
- This is where I encounter my issue. The transfer function provided by the manufacturer is very clean. However, when I add the OTA output impedance, my transfer function grows in size. The poles are no longer a simple fraction, but rather incorporate every component of the compensator.
- This does make sense to me (after all, the OTA impedance 'sees' the whole network and not only one capacitor). Furthermore, the manufacturer also mentions simplifying the transfer function as well.
- However, I cannot find a full derivation of the type II compensator anywhere on the internet. So, keeping the above in mind, my questions are:
- * What is the accurate transfer function for this circuit?
- * Why can we calculate the influence of the output impedance taking only the Cth capacitor into account?
- I would appreciate any help with this question as I have been wrestling with this transfer function for a while now.
#1: Initial revision
Type II compensation network for a non-ideal transconductance amplifier
I am designing a DC/DC converter in the control loop of which a transconductance amplifier (OTA) is used. This part of circuit looks like this:  To determine the needed characteristics, I am using a transfer function provided by the manufacturer (AD). However, today I decided to check the transfer function by hand and encountered a roadblock. The manufacturer (and other sources) say that the transfer function is:  where: * `s_thz = 1/(Rth*Cth)`, zero contributed by the resistor * `s_po = 1/(Ro*Cth)`, pole contributed by the op-amp input resistance and `Cth` * `s_thp = 1/(Ro*Cth)`, high-frequency pole contributed by the `Cthp` capacitor I could derive the transfer function for the network of `Cth, Rth` and `Cthp` with no issue. I observe the high-frequency pole, a zero and a pole at origin typical of those configurations. However, as the [application note discussing compensation networks](https://www.analog.com/media/en/technical-documentation/application-notes/an149fa.pdf) points out, the OTA is not ideal and so its impedance wil move the pole off of the origin. It is still a low- frequency pole, but the 'pole at origin' model becomes inaccurate. This is where I encounter my issue. The transfer function provided by the manufacturer is very clean. However, when I add the OTA output impedance, my transfer function grows in size. The poles are no longer a simple fraction, but rather incorporate every component of the compensator. This does make sense to me (after all, the OTA impedance 'sees' the whole network and not only one capacitor). Furthermore, the manufacturer also mentions simplifying the transfer function as well. However, I cannot find a full derivation of the type II compensator anywhere on the internet. So, keeping the above in mind, my questions are: * What is the accurate transfer function for this circuit? * Why can we calculate the influence of the output impedance taking only the Cth capacitor into account? I would appreciate any help with this question as I have been wrestling with this transfer function for a while now.


















