Post History

If you are pursuing engineering then you can't use doodles instead of schematics generated by dedicated (or not) programs. It will take you just the same amount of time, if not less, and the results would be clear for anyone seeing them.

The basic schematic of the Hartley oscillator can be simplified, for the purpose of analysis: the base resistors can be considered much larger than the input resistance of the transistor, so they can be eliminated, the coupling capacitors can be considered to give a sufficient bandwidth to not influence the response, so they can be shorted out, and the emitter and collector resistors, together with the load (resistance, not impedance, simplification for the sake of analysis) and internal resistance can be combined into one resistance. Now you can redraw the circuit like this:

![equivalent small signal](https://electrical.codidact.com/uploads/fdDud88XJzhQtSZpmzaL9LWi)

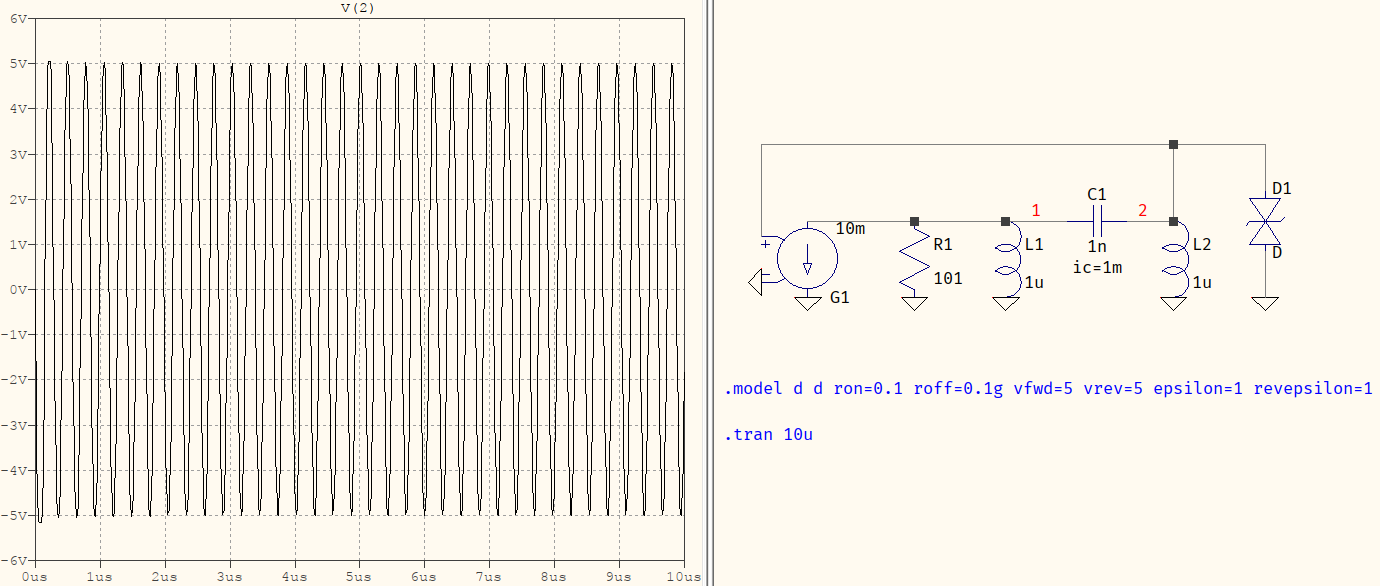
Given some small initial conditions, the circuit can be verified that it works. `D1` is there to limit the amplitude, since the whole circuit would be linear, otherwise, and the oscillations would rise to infinity.

Note that $g_m$=0.01 and the load resistor is 101 Ω -- that is part of the necessary condition for the oscillations to start and be sustained (I'll show below). Here, the resistor is 101 Ω to compensate for the slight parasitics in inductors, capacitor, and the OFF resistance of the diode.

Now you can write down the equations Kirchhoff, out of which only one of them is of interest:

$$\begin{align}
V_2\left(\dfrac{1}{sL}+sC\right)&=V_1sC \\\\
\Rightarrow\quad V_2&=V_1\dfrac{sC}{\dfrac{1}{sL}+sC} \\\\
\Rightarrow\quad V_2&=V_1\dfrac{s^2LC}{s^2LC+1} \tag{1}
\end{align}$$

The energies at the output of the transistor and the input to the tank must satisfy:

$$\begin{align}
(-g_mV_2)V_1t&\ge\dfrac{V_1^2}{R}t \tag{2} \\\\
(-g_mV_1\dfrac{s^2L_2C}{s^2L_2C+1})V_1t&\ge\dfrac{V_1^2}{R}t \\\\
-g_mV_1^2\dfrac{s^2L_2C}{s^2L_2C+1}t&\ge\dfrac{V_1^2}{R}t\quad\Biggr|_{\div V_1^2t} \\\\
\Rightarrow\quad -g_m\dfrac{s^2L_2C}{s^2L_2C+1}&\ge\dfrac{1}{R}
\end{align}$$

At this point it's useful to eliminate the frequency by substituting $s^2=-\omega^2$, and using $\omega^2=1/[2C(L_1+L_2)]$:

$$\begin{align}
g_m\dfrac{\dfrac{L_2}{L_1+L_2}}{1-\dfrac{L_2}{L_1+L_2}}&\ge\dfrac1R \\\\
\Rightarrow\quad g_m\dfrac{L_2}{L_1}\ge\dfrac1R \tag{3}
\end{align}$$

Which is the condition for oscillation. In your OP you wrote that the ratio of the output to the input voltage is 1, but it should be -1, since they're in anti-phase. If you want to include $Z_L$ in the equation, and the rest, feel free to do so, it will only add to the complexity, but this is the base of it.