Post History
The website that I mentioned before mentions the max flux density in ferrites at 400 kHz as being close to 0.04 T. Is this correct? No, you have misinterpreted the graph. The graph shown is fl...
#3: Post edited
- > _The website that I mentioned before mentions the max flux density in ferrites at 400 kHz as being close to 0.04 T. Is this correct?_
- No, you have misinterpreted the graph. The graph shown is flux density (not maximum flux density) and is only telling you one thing; that if you increase the frequency of an applied voltage on an inductor by "X" then the current into that inductor reduces by "X". Correspondingly, flux density also falls by "X".
- > _Is the chosen current density correct? Also, will there be any issue due to more number of strands (more than the required value) within the wire? Should I use litz wire or just stick to using a solid core AWG 28 wire instead?_
- I think you are going down the wrong route for this job. For instance, you have chosen a topology (an LLC series resonant type) that is overly complex for a paltry 1 watt output. You should have considered a flyback topology first because they are the simplest to implement, require only one driving MOSFET and are perfectly good at providing the necessary isolation levels.
- Nevertheless, I shall attempt to point you in a direction regarding the calculation of peak flux density because the following can apply to both topologies.
- You have said (in comments) [that the load is 100 Ω](https://electrical.codidact.com/comments/thread/8917#comment-22809). You have also said that the power output is 1 watt. So, this means that the output voltage is 10 volts RMS. Given that the turns ratio is 15:10, this means that the input voltage is 15 volts RMS.
- It's vital to know what the input voltage is because you need this to calculate the peak flux density in the core. You then link the core-set data sheet and, for N49 material, a core set is available that is gapped: -
- 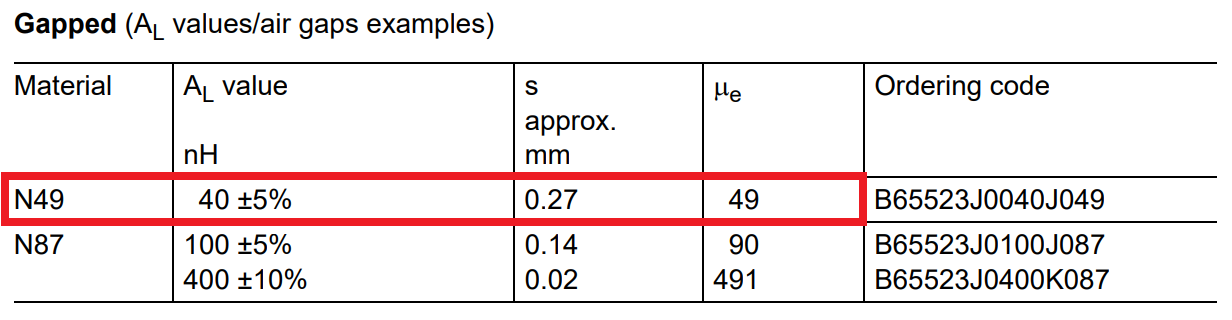
- It has an \$A_L\$ factor of 40 nH. This means that the primary inductance is 40 nH × 15 turns × 15 turns = 9 μH. The primary magnetization current will peak at: -
- $$\dfrac{V}{L}\cdot dt = di$$
- di is the change in current from 0 when dt is half the period of 400 kHz hence, di = 2.08 amps. This assumes that the applied primary voltage is a square wave of peak value 15 volts. It's really not clear from your question whether this is a million miles away from being true.
- The H-field will 2.08 amps x 15 turns divided by the mean length of the core (in metres). This comes to 2,298 At/m. You have a core permeability (gapped) of 49 hence the peak flux density of this circuit will be: -
- $$4\pi \times 10^{-7} \times 49 \times 2298 = 141 \text{ mT}$$
Once you have this figure (a decent figure) you can begin to choose your wires but, it's highly unlikely that you will need Litz wire.
- > _The website that I mentioned before mentions the max flux density in ferrites at 400 kHz as being close to 0.04 T. Is this correct?_
- No, you have misinterpreted the graph. The graph shown is flux density (not maximum flux density) and is only telling you one thing; that if you increase the frequency of an applied voltage on an inductor by "X" then the current into that inductor reduces by "X". Correspondingly, flux density also falls by "X".
- > _Is the chosen current density correct? Also, will there be any issue due to more number of strands (more than the required value) within the wire? Should I use litz wire or just stick to using a solid core AWG 28 wire instead?_
- I think you are going down the wrong route for this job. For instance, you have chosen a topology (an LLC series resonant type) that is overly complex for a paltry 1 watt output. You should have considered a flyback topology first because they are the simplest to implement, require only one driving MOSFET and are perfectly good at providing the necessary isolation levels.
- Nevertheless, I shall attempt to point you in a direction regarding the calculation of peak flux density because the following can apply to both topologies.
- You have said (in comments) [that the load is 100 Ω](https://electrical.codidact.com/comments/thread/8917#comment-22809). You have also said that the power output is 1 watt. So, this means that the output voltage is 10 volts RMS. Given that the turns ratio is 15:10, this means that the input voltage is 15 volts RMS.
- It's vital to know what the input voltage is because you need this to calculate the peak flux density in the core. You then link the core-set data sheet and, for N49 material, a core set is available that is gapped: -
- 
- It has an \$A_L\$ factor of 40 nH. This means that the primary inductance is 40 nH × 15 turns × 15 turns = 9 μH. The primary magnetization current will peak at: -
- $$\dfrac{V}{L}\cdot dt = di$$
- di is the change in current from 0 when dt is half the period of 400 kHz hence, di = 2.08 amps. This assumes that the applied primary voltage is a square wave of peak value 15 volts. It's really not clear from your question whether this is a million miles away from being true.
- The H-field will 2.08 amps x 15 turns divided by the mean length of the core (in metres). This comes to 2,298 At/m. You have a core permeability (gapped) of 49 hence the peak flux density of this circuit will be: -
- $$4\pi \times 10^{-7} \times 49 \times 2298 = 141 \text{ mT}$$
- Once you have this figure (a decent figure for a flyback circuit) you can begin to choose your wires but, it's highly unlikely that you will need Litz wire. For a resonant converter it's not a bad figure but, you might do better choosing an un-gapped core set and keep the magnetization current lower (due to significantly higher inductance for the same number of turns). I mean you have a peak primary current (no load) of 2.08 amps and the RMS will be root-3 lower at 1.2 amps. If the core was un-gapped, this figure would drop considerably (a good thing for an LLC series resonant converter).
#2: Post edited
- > _The website that I mentioned before mentions the max flux density in ferrites at 400 kHz as being close to 0.04 T. Is this correct?_
- No, you have misinterpreted the graph. The graph shown is flux density (not maximum flux density) and is only telling you one thing; that if you increase the frequency of an applied voltage on an inductor by "X" then the current into that inductor reduces by "X". Correspondingly, flux density also falls by "X".
- > _Is the chosen current density correct? Also, will there be any issue due to more number of strands (more than the required value) within the wire? Should I use litz wire or just stick to using a solid core AWG 28 wire instead?_
- I think you are going down the wrong route for this job. For instance, you have chosen a topology (an LLC series resonant type) that is overly complex for a paltry 1 watt output. You should have considered a flyback topology first because they are the simplest to implement, require only one driving MOSFET and are perfectly good at providing the necessary isolation levels.
- Nevertheless, I shall attempt to point you in a direction regarding the calculation of peak flux density because the following can apply to both topologies.
- You have said (in comments) [that the load is 100 Ω](https://electrical.codidact.com/comments/thread/8917#comment-22809). You have also said that the power output is 1 watt. So, this means that the output voltage is 10 volts RMS. Given that the turns ratio is 15:10, this means that the input voltage is 15 volts RMS.
- It's vital to know what the input voltage is because you need this to calculate the peak flux density in the core. You then link the core-set data sheet and, for N49 material, a core set is available that is gapped: -
- 
- It has an \$A_L\$ factor of 40 nH. This means that the primary inductance is 40 nH × 15 turns × 15 turns = 9 μH. The primary magnetization current will peak at: -
- $$\dfrac{V}{L}\cdot dt = di$$
- di is the change in current from 0 when dt is half the period of 400 kHz hence, di = 2.08 amps. This assumes that the applied primary voltage is a square wave of peak value 15 volts. It's really not clear from your question whether this is a million miles away from being true.
- The H-field will 2.08 amps x 15 turns divided by the mean length of the core (in metres). This comes to 2,298 At/m. You have a core permeability (gapped) of 49 hence the peak flux density of this circuit will be: -
$$4\pi \times 10^{-7} \times 49 \times 2298 = 141 mT$$- Once you have this figure (a decent figure) you can begin to choose your wires but, it's highly unlikely that you will need Litz wire.
- > _The website that I mentioned before mentions the max flux density in ferrites at 400 kHz as being close to 0.04 T. Is this correct?_
- No, you have misinterpreted the graph. The graph shown is flux density (not maximum flux density) and is only telling you one thing; that if you increase the frequency of an applied voltage on an inductor by "X" then the current into that inductor reduces by "X". Correspondingly, flux density also falls by "X".
- > _Is the chosen current density correct? Also, will there be any issue due to more number of strands (more than the required value) within the wire? Should I use litz wire or just stick to using a solid core AWG 28 wire instead?_
- I think you are going down the wrong route for this job. For instance, you have chosen a topology (an LLC series resonant type) that is overly complex for a paltry 1 watt output. You should have considered a flyback topology first because they are the simplest to implement, require only one driving MOSFET and are perfectly good at providing the necessary isolation levels.
- Nevertheless, I shall attempt to point you in a direction regarding the calculation of peak flux density because the following can apply to both topologies.
- You have said (in comments) [that the load is 100 Ω](https://electrical.codidact.com/comments/thread/8917#comment-22809). You have also said that the power output is 1 watt. So, this means that the output voltage is 10 volts RMS. Given that the turns ratio is 15:10, this means that the input voltage is 15 volts RMS.
- It's vital to know what the input voltage is because you need this to calculate the peak flux density in the core. You then link the core-set data sheet and, for N49 material, a core set is available that is gapped: -
- 
- It has an \$A_L\$ factor of 40 nH. This means that the primary inductance is 40 nH × 15 turns × 15 turns = 9 μH. The primary magnetization current will peak at: -
- $$\dfrac{V}{L}\cdot dt = di$$
- di is the change in current from 0 when dt is half the period of 400 kHz hence, di = 2.08 amps. This assumes that the applied primary voltage is a square wave of peak value 15 volts. It's really not clear from your question whether this is a million miles away from being true.
- The H-field will 2.08 amps x 15 turns divided by the mean length of the core (in metres). This comes to 2,298 At/m. You have a core permeability (gapped) of 49 hence the peak flux density of this circuit will be: -
- $$4\pi \times 10^{-7} \times 49 \times 2298 = 141 \text{ mT}$$
- Once you have this figure (a decent figure) you can begin to choose your wires but, it's highly unlikely that you will need Litz wire.
#1: Initial revision
> _The website that I mentioned before mentions the max flux density in ferrites at 400 kHz as being close to 0.04 T. Is this correct?_
No, you have misinterpreted the graph. The graph shown is flux density (not maximum flux density) and is only telling you one thing; that if you increase the frequency of an applied voltage on an inductor by "X" then the current into that inductor reduces by "X". Correspondingly, flux density also falls by "X".
> _Is the chosen current density correct? Also, will there be any issue due to more number of strands (more than the required value) within the wire? Should I use litz wire or just stick to using a solid core AWG 28 wire instead?_
I think you are going down the wrong route for this job. For instance, you have chosen a topology (an LLC series resonant type) that is overly complex for a paltry 1 watt output. You should have considered a flyback topology first because they are the simplest to implement, require only one driving MOSFET and are perfectly good at providing the necessary isolation levels.
Nevertheless, I shall attempt to point you in a direction regarding the calculation of peak flux density because the following can apply to both topologies.
You have said (in comments) [that the load is 100 Ω](https://electrical.codidact.com/comments/thread/8917#comment-22809). You have also said that the power output is 1 watt. So, this means that the output voltage is 10 volts RMS. Given that the turns ratio is 15:10, this means that the input voltage is 15 volts RMS.
It's vital to know what the input voltage is because you need this to calculate the peak flux density in the core. You then link the core-set data sheet and, for N49 material, a core set is available that is gapped: -

It has an \$A_L\$ factor of 40 nH. This means that the primary inductance is 40 nH × 15 turns × 15 turns = 9 μH. The primary magnetization current will peak at: -
$$\dfrac{V}{L}\cdot dt = di$$
di is the change in current from 0 when dt is half the period of 400 kHz hence, di = 2.08 amps. This assumes that the applied primary voltage is a square wave of peak value 15 volts. It's really not clear from your question whether this is a million miles away from being true.
The H-field will 2.08 amps x 15 turns divided by the mean length of the core (in metres). This comes to 2,298 At/m. You have a core permeability (gapped) of 49 hence the peak flux density of this circuit will be: -
$$4\pi \times 10^{-7} \times 49 \times 2298 = 141 mT$$
Once you have this figure (a decent figure) you can begin to choose your wires but, it's highly unlikely that you will need Litz wire.


















