Post History
Noise can be coupled between signal lines through parasitic capacitance formed between these signal lines, as $i = C\frac{dv}{dt}$ where C is the capacitance between the signal lines. Another wa...
#3: Post edited
- Noise can be coupled between signal lines through parasitic capacitance formed between these signal lines, as
- $i = C\frac{dv}{dt}$
- where C is the capacitance between the signal lines.
- Another way of noise coupling into signal lines is through inductive coupling, where changing magnetic field induces current into the adjacent signal line:
- $v = L\frac{di}{dt}$
L being mutual inductance, and di being change of current in the aggressor line.To reduce noise sensitivity of the victim lines, capacitors can be placed on them, providing a low impedance return path. Capacitor impedance is frequency dependent, and effectively goes down up until the resonance frequency, at which point parasitic inductance becomes dominating, therefore it would be useful to pick a capacitor that has the lowest impedance at the frequencies present in the system.- However, it is the rate of change that causes the problem, so a 1kHz square wave with 10ps rise time could cause considerably more issues than a 1kHz square wave with 100us rise time.
- Hence my question, if I know the rise times of certain signals in the system, how can I evaluate the frequency and therefore the appropriate type and value of capacitors to provide a low impedance path for a particular frequency?
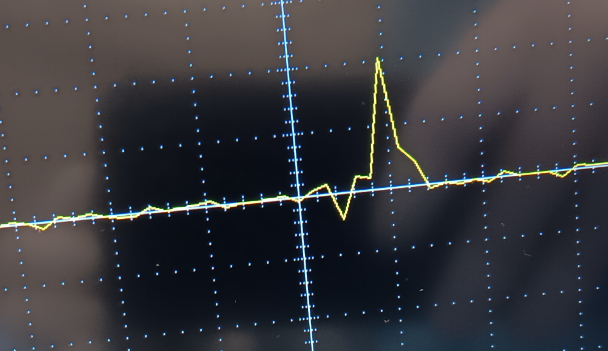
- For example, if there is a recurring noise spike like this:
- 
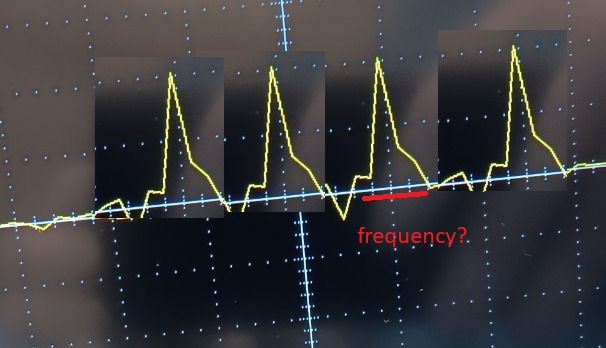
- Would it be appropriate to imagine it as a periodic signal and see it as:
- 
- The importance of this can be seen as the rise times of integrated circuits are getting considerably faster as technology advances and dies are shrinking. Rick Hartley illustrated how closely coupled power and ground planes can provide low impedance path at frequencies where capacitors are no longer useful: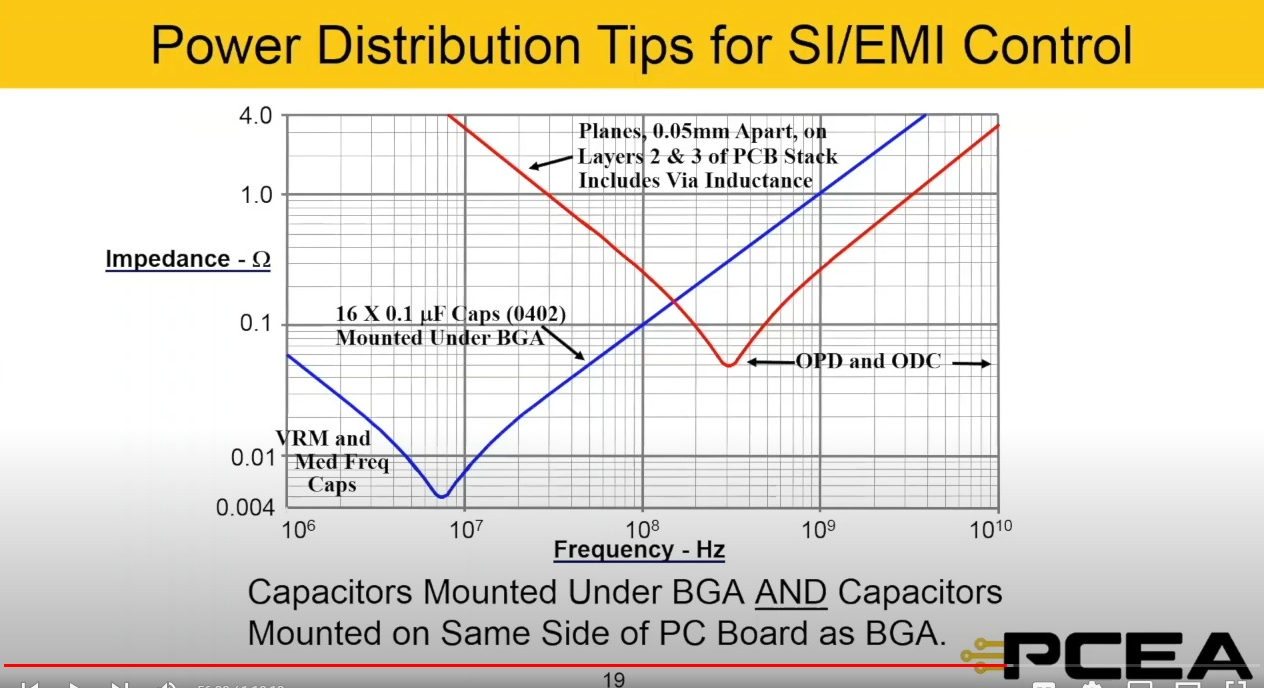
- In the particular lecture it was in respect to power delivery, however, (I think) it also applies to noise filtering.
- Any thoughts and suggestions are appreciated!
- Noise can be coupled between signal lines through parasitic capacitance formed between these signal lines, as
- $i = C\frac{dv}{dt}$
- where C is the capacitance between the signal lines.
- Another way of noise coupling into signal lines is through inductive coupling, where changing magnetic field induces current into the adjacent signal line:
- $v = L\frac{di}{dt}$
- L being mutual inductance, and di being change of current in the aggressor line. To reduce noise sensitivity of the victim lines, capacitors can be placed on them, providing a low impedance return path. Capacitor impedance is frequency dependent, and effectively goes down up until the resonance frequency, at which point parasitic inductance becomes dominating, therefore it would be useful to pick a capacitor that has the lowest impedance at the frequencies present in the system.
- However, it is the rate of change that causes the problem, so a 1kHz square wave with 10ps rise time could cause considerably more issues than a 1kHz square wave with 100us rise time.
- Hence my question, if I know the rise times of certain signals in the system, how can I evaluate the frequency and therefore the appropriate type and value of capacitors to provide a low impedance path for a particular frequency?
- For example, if there is a recurring noise spike like this:
- 
- Would it be appropriate to imagine it as a periodic signal and see it as:
- 
- The importance of this can be seen as the rise times of integrated circuits are getting considerably faster as technology advances and dies are shrinking. Rick Hartley illustrated how closely coupled power and ground planes can provide low impedance path at frequencies where capacitors are no longer useful:
- In the particular lecture it was in respect to power delivery, however, (I think) it also applies to noise filtering.
- Any thoughts and suggestions are appreciated!
#2: Post edited
- Noise can be coupled between signal lines through parasitic capacitance formed between these signal lines, as
- $i = C\frac{dv}{dt}$
- where C is the capacitance between the signal lines.
- Another way of noise coupling into signal lines is through inductive coupling, where changing magnetic field induces current into the adjacent signal line:
- $v = L\frac{di}{dt}$
To reduce noise sensitivity of the victim lines, capacitors can be placed on them, providing a low impedance return path. Capacitor impedance is frequency dependent, and effectively goes down up until the resonance frequency, at which point parasitic inductance becomes dominating, therefore it would be useful to pick a capacitor that has the lowest impedance at the frequencies present in the system.- However, it is the rate of change that causes the problem, so a 1kHz square wave with 10ps rise time could cause considerably more issues than a 1kHz square wave with 100us rise time.
- Hence my question, if I know the rise times of certain signals in the system, how can I evaluate the frequency and therefore the appropriate type and value of capacitors to provide a low impedance path for a particular frequency?
- For example, if there is a recurring noise spike like this:
- 
- Would it be appropriate to imagine it as a periodic signal and see it as:
- 
- The importance of this can be seen as the rise times of integrated circuits are getting considerably faster as technology advances and dies are shrinking. Rick Hartley illustrated how closely coupled power and ground planes can provide low impedance path at frequencies where capacitors are no longer useful:
- In the particular lecture it was in respect to power delivery, however, (I think) it also applies to noise filtering.
- Any thoughts and suggestions are appreciated!
- Noise can be coupled between signal lines through parasitic capacitance formed between these signal lines, as
- $i = C\frac{dv}{dt}$
- where C is the capacitance between the signal lines.
- Another way of noise coupling into signal lines is through inductive coupling, where changing magnetic field induces current into the adjacent signal line:
- $v = L\frac{di}{dt}$
- L being mutual inductance, and di being change of current in the aggressor line.To reduce noise sensitivity of the victim lines, capacitors can be placed on them, providing a low impedance return path. Capacitor impedance is frequency dependent, and effectively goes down up until the resonance frequency, at which point parasitic inductance becomes dominating, therefore it would be useful to pick a capacitor that has the lowest impedance at the frequencies present in the system.
- However, it is the rate of change that causes the problem, so a 1kHz square wave with 10ps rise time could cause considerably more issues than a 1kHz square wave with 100us rise time.
- Hence my question, if I know the rise times of certain signals in the system, how can I evaluate the frequency and therefore the appropriate type and value of capacitors to provide a low impedance path for a particular frequency?
- For example, if there is a recurring noise spike like this:
- 
- Would it be appropriate to imagine it as a periodic signal and see it as:
- 
- The importance of this can be seen as the rise times of integrated circuits are getting considerably faster as technology advances and dies are shrinking. Rick Hartley illustrated how closely coupled power and ground planes can provide low impedance path at frequencies where capacitors are no longer useful:
- In the particular lecture it was in respect to power delivery, however, (I think) it also applies to noise filtering.
- Any thoughts and suggestions are appreciated!
#1: Initial revision
How to convert dv/dt of noise into frequency for filter capacitor selection?
Noise can be coupled between signal lines through parasitic capacitance formed between these signal lines, as
$i = C\frac{dv}{dt}$
where C is the capacitance between the signal lines.
Another way of noise coupling into signal lines is through inductive coupling, where changing magnetic field induces current into the adjacent signal line:
$v = L\frac{di}{dt}$
To reduce noise sensitivity of the victim lines, capacitors can be placed on them, providing a low impedance return path. Capacitor impedance is frequency dependent, and effectively goes down up until the resonance frequency, at which point parasitic inductance becomes dominating, therefore it would be useful to pick a capacitor that has the lowest impedance at the frequencies present in the system.
However, it is the rate of change that causes the problem, so a 1kHz square wave with 10ps rise time could cause considerably more issues than a 1kHz square wave with 100us rise time.
Hence my question, if I know the rise times of certain signals in the system, how can I evaluate the frequency and therefore the appropriate type and value of capacitors to provide a low impedance path for a particular frequency?
For example, if there is a recurring noise spike like this:

Would it be appropriate to imagine it as a periodic signal and see it as:

The importance of this can be seen as the rise times of integrated circuits are getting considerably faster as technology advances and dies are shrinking. Rick Hartley illustrated how closely coupled power and ground planes can provide low impedance path at frequencies where capacitors are no longer useful:
In the particular lecture it was in respect to power delivery, however, (I think) it also applies to noise filtering.
Any thoughts and suggestions are appreciated!


















